题目内容
设三个不相等的有理数a，b，c满足a+b+c=0，则a，b，c中正数的个数为 ．
考点：有理数的加法
专题：
分析：由于三个不相等的有理数a，b，c满足a+b+c=0，可以分两种情况得到正数的个数．
解答：解：∵三个不相等的有理数a，b，c满足a+b+c=0，
∴a，b，c中正数的个数为2个或1个．
故答案为：2个或1个．
∴a，b，c中正数的个数为2个或1个．
故答案为：2个或1个．
点评：此题主要利用了有理数的计算法则，注意分类思想的运用．
练习册系列答案
智能训练练测考系列答案
相关题目
两个同心圆，小圆半径2cm，大圆半径4cm，点Q在圆环内无规则自由运动，如果在某一时刻突然停下来，那么点Q与点O距离小于3cm的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，点A、B、C、D都在⊙O上，∠DEB=85°，∠B=35°，则∠A为（ ）| A、30° | B、45° |
| C、50° | D、60° |
如图，在△ABC中，PM、QN分别是AB、AC的垂直平分线，∠PAQ=30°，那么∠BAC等于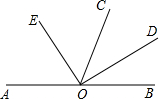
如图，O是直线AB上一点，OC为任一条射线，OD平分∠BOC，OE平分∠AOC．