题目内容
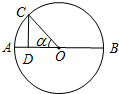 如图,AB为⊙O的直径,D为AB上一点,且AB=6AD,CD⊥AB于D,C在⊙O上,设∠COD=α,则tan
如图,AB为⊙O的直径,D为AB上一点,且AB=6AD,CD⊥AB于D,C在⊙O上,设∠COD=α,则tan| α |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:圆周角定理,解直角三角形
专题:计算题
分析:连结BC、AD,如图,设AD=x,则AB=6x,OA=OB=OC=3x,OD=OA-AD=2x,在Rt△OCD中利用勾股定理计算出CD=
x,再在Rt△BCD中,利用正切的定义得tanB=
=
,然后证明∠B=
α即可得到答案.
| 5 |
| CD |
| BD |
| ||
| 5 |
| 1 |
| 2 |
解答:解:连结BC、AD,如图, 设AD=x,则AB=6x,OA=OB=OC=3x,OD=OA-AD=2x,
设AD=x,则AB=6x,OA=OB=OC=3x,OD=OA-AD=2x,
在Rt△OCD中,∵OD=2x,OC=3x,
∴CD=
=
x,
在Rt△BCD中,tanB=
=
=
,
∵OB=OC,
∴∠B=∠OCB,
而∠COD=∠B+∠C=α,
∴tan
=
.
故选B.
 设AD=x,则AB=6x,OA=OB=OC=3x,OD=OA-AD=2x,
设AD=x,则AB=6x,OA=OB=OC=3x,OD=OA-AD=2x,在Rt△OCD中,∵OD=2x,OC=3x,
∴CD=
| OC2-OD2 |
| 5 |
在Rt△BCD中,tanB=
| CD |
| BD |
| ||
| 2x+3x |
| ||
| 5 |
∵OB=OC,
∴∠B=∠OCB,
而∠COD=∠B+∠C=α,
∴tan
| α |
| 2 |
| ||
| 5 |
故选B.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了解直角三角形.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,点A、B、C、D都在⊙O上,∠DEB=85°,∠B=35°,则∠A为( )
如图,点A、B、C、D都在⊙O上,∠DEB=85°,∠B=35°,则∠A为( )| A、30° | B、45° |
| C、50° | D、60° |
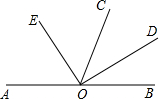 如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.