题目内容
7.已知反比例函数y=-$\frac{8}{x}$,则下列各点在此函数图象上的是( )| A. | (2,4) | B. | (-1,-8) | C. | (-2,-4) | D. | (4,-2) |
分析 把点的坐标代入反比例函数的解析式,判断即可.
解答 解:当x=2时,y=-4,
则(2,4)不在反比例函数y=-$\frac{8}{x}$的图象上,
当x=-1时,y=8,
则(-1,-8)不在反比例函数y=-$\frac{8}{x}$的图象上,
当x=-2时,y=4,
则(-2,-4)不在反比例函数y=-$\frac{8}{x}$的图象上,
当x=4时,y=-2,
则(4,-2)在反比例函数y=-$\frac{8}{x}$的图象上,
故选:D.
点评 本题考查的是反比例函数图象上点的坐标特征,掌握反比例函数图象上点的坐标满足反比例函数的解析式是解题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
17.为了迎接“端午”小长假的购物高峰,某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)专卖店计划购进的甲、乙两种运动鞋共200双,总进价不低于17600元,且不超过17660元,问该专卖店有哪几种进货方案?
(3)在(2)的条件下,求该专卖店要获得最大利润的进货方案及最大利润.
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 160 | 150 |
(1)求m的值;
(2)专卖店计划购进的甲、乙两种运动鞋共200双,总进价不低于17600元,且不超过17660元,问该专卖店有哪几种进货方案?
(3)在(2)的条件下,求该专卖店要获得最大利润的进货方案及最大利润.
18.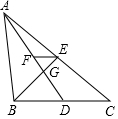 如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,则FG:AG是( )
如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,则FG:AG是( )
 如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,则FG:AG是( )
如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,则FG:AG是( )| A. | 1:4 | B. | 1:3 | C. | 1:2 | D. | 2:3 |
16.$\frac{1}{3}$的绝对值是( )
| A. | $-\frac{1}{3}$ | B. | -3 | C. | 3 | D. | $\frac{1}{3}$ |
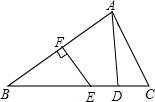 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.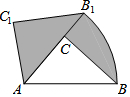 如图,在△ACB中,∠BAC=50°,AC=4,AB=6.现将△ACB绕点A逆时针旋转50°得到△AC1B1则阴影部分的面积为5π.
如图,在△ACB中,∠BAC=50°,AC=4,AB=6.现将△ACB绕点A逆时针旋转50°得到△AC1B1则阴影部分的面积为5π.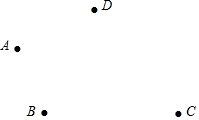 如图,平面上有四个点A,B,C,D,按照以下要求完成问题:
如图,平面上有四个点A,B,C,D,按照以下要求完成问题: