题目内容
17.为了迎接“端午”小长假的购物高峰,某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 160 | 150 |
(1)求m的值;
(2)专卖店计划购进的甲、乙两种运动鞋共200双,总进价不低于17600元,且不超过17660元,问该专卖店有哪几种进货方案?
(3)在(2)的条件下,求该专卖店要获得最大利润的进货方案及最大利润.
分析 (1)根据:甲运动鞋的总成本÷甲运动鞋的进价=乙运动鞋的总成本÷乙运动鞋的进价,列分式方程求解可得;
(2)设购进甲运动鞋x双,则乙运动鞋(200-x)双,根据“17600≤甲运动鞋的总成本+乙运动鞋的总成本≤17660”列不等式组求解可得;
(3)设专卖店获得的利润为W,根据“总利润=甲运动鞋的总利润+乙运动鞋的总利润”列出函数解析式,根据一次函数的性质求得最值即可得.
解答 解:(1)根据题意,得:$\frac{3000}{m}$=$\frac{2400}{m-20}$,
解得:m=100,
经检验:m=100是分式方程的解,
∴m=100;
(2)设购进甲运动鞋x双,则乙运动鞋(200-x)双,
根据题意得:$\left\{\begin{array}{l}{100x+80(200-x)≥17600}\\{100x+80(20-x)≤17660}\end{array}\right.$,
解得:80≤x≤83,
∴购进的方案有:
方案一:购进甲运动鞋80双,乙运动鞋120双;
方案二:购进甲运动鞋81双,乙运动鞋119双;
方案三:购进甲运动鞋82双,乙运动鞋118双;
方案四:购进甲运动鞋83双,乙运动鞋117双.
(3)设专卖店获得的利润为W,
则W=(160-100)x+(150-80)(200-x)
=-10x+14000,
∵W随x的增大而减小,且80≤x≤83,x为整数,
∴当x=80时,W取得大值,最大值为13200元,
答:当该专卖店购进甲运动鞋80双、乙运动鞋120双获得的利润最大,最大利润为13200元.
点评 本题主要考查分式方程、一元一次不等式组和一次函数的应用,理解题意找到题目蕴含的相等关系或不等关系是解应用题的关键.

练习册系列答案
相关题目
9.计算-2x(x2-1)的结果是( )
| A. | -2x3-2x | B. | -2x3+x | C. | -2x3+2x | D. | -x3+2x |
7.已知反比例函数y=-$\frac{8}{x}$,则下列各点在此函数图象上的是( )
| A. | (2,4) | B. | (-1,-8) | C. | (-2,-4) | D. | (4,-2) |
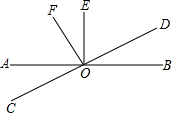 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD. 如图所示的几何体是由9个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由9个小正方体组合而成的,它的左视图是( )



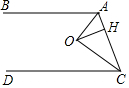 如图,AB∥CD,OA,OC分别平分∠BAC和∠ACD,OH⊥AC于点H,且OH=4,则AB,CD之间的距离为8.
如图,AB∥CD,OA,OC分别平分∠BAC和∠ACD,OH⊥AC于点H,且OH=4,则AB,CD之间的距离为8.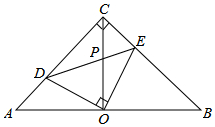 如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )