题目内容
19.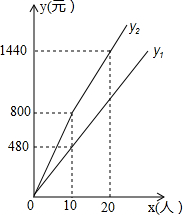 盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.(1)a=6,b=8;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到红海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
分析 (1)根据函数图象,用购票款数除以定价的款数,计算即可求出a的值;用第11人到20人的购票款数除以定价的款数,计算即可求出b的值;
(2)利用待定系数法求正比例函数解析式求出y1,分x≤10与x>10,利用待定系数法求一次函数解析式求出y2与x的函数关系式即可;
(3)设A团有n人,表示出B团的人数为(50-n),然后分0≤n≤10与n>10两种情况,根据(2)的函数关系式列出方程求解即可.
解答 解:(1)由y1图象上点(10,480),得到10人的费用为480元,
∴a=$\frac{480}{800}$×10=6;
由y2图象上点(10,800)和(20,1440),得到20人中后10人费用为640元,
∴b=$\frac{640}{800}$×10=8;
(2)设y1=k1x,
∵函数图象经过点(0,0)和(10,480),
∴10k1=480,
∴k1=48,
∴y1=48x;
0≤x≤10时,设y2=k2x,
∵函数图象经过点(0,0)和(10,800),
∴10k2=800,
∴k2=80,
∴y2=80x,
x>10时,设y2=kx+b,
∵函数图象经过点(10,800)和(20,1440),
∴$\left\{\begin{array}{l}{10k+b=800}\\{20k+b=1440}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=64}\\{b=160}\end{array}\right.$,
∴y2=64x+160;
∴y2=$\left\{\begin{array}{l}{80x(0≤x≤10)\\;}\\{64x+160(x>10)}\end{array}\right.$;
(3)设B团有n人,则A团的人数为(50-n),
当0≤n≤10时,80n+48×(50-n)=3040,
解得n=20(不符合题意舍去),
当n>10时,800+64×(n-10)+48×(50-n)=3040,
解得n=30,
则50-n=50-30=20.
答:A团有20人,B团有30人.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,准确识图获取必要的信息并理解打折的意义是解题的关键,(3)要注意分情况讨论.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案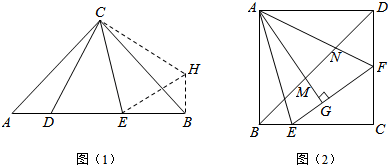
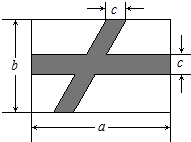 如图,长方形中,横向阴影部分为长方形,另一阴影部分为平行四边形,根据图中标注的数据,可计算空白部分的面积是ab-ac-bc+c2.
如图,长方形中,横向阴影部分为长方形,另一阴影部分为平行四边形,根据图中标注的数据,可计算空白部分的面积是ab-ac-bc+c2.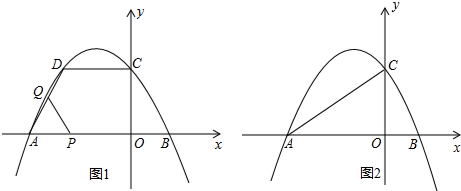
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则由抛物线的特征可得到含a,b,c三个字母的等式或不等式为a-b+c>0.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则由抛物线的特征可得到含a,b,c三个字母的等式或不等式为a-b+c>0. 如图,△ABC的三条中线AD,BE,CF交于点O,且AD=5,则AO=$\frac{5}{3}$.
如图,△ABC的三条中线AD,BE,CF交于点O,且AD=5,则AO=$\frac{5}{3}$.