题目内容
5．2013减去它的$\frac{1}{2}$，再减去剩余的$\frac{1}{3}$，再减去剩余数的$\frac{1}{4}$，以此类推…．一直到减去剩余数的$\frac{1}{2013}$，那么最后剩余数为1．分析 由题意可列出：2013×（1-$\frac{1}{2}$）×（1-$\frac{1}{3}$）×（1-$\frac{1}{4}$）×…×（1-$\frac{1}{2013}$），然后计算即可．
解答 解：由题意可列出：
2013×（1-$\frac{1}{2}$）×（1-$\frac{1}{3}$）×（1-$\frac{1}{4}$）×…×（1-$\frac{1}{2013}$）
=2013×$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{2012}{2013}$
=1．
故答案为：1．
点评 此题主要考查了有理数的混合运算，根据题意列出算式是解本题的关键．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
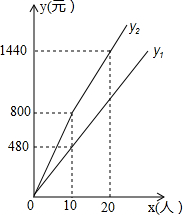盘锦红海滩景区门票价格80元/人，景区为吸引游客，对门票价格进行动态管理，非节假日打a折，节假日期间，10人以下（包括10人）不打折，10人以上超过10人的部分打b折，设游客为x人，门票费用为y元，非节假日门票费用y1（元）及节假日门票费用y2（元）与游客x（人）之间的函数关系如图所示．
17．
“无字证明”（proofs without words），就是将数学命题用简单、有创意而且易于理解的几何图形来呈现．现将边长为a的正方形挖去一个边长为b的小正方形（a＞b）（如图甲），把剩下的部分拼成一个矩形（如图乙）．根据这两个图形中阴影部分的面积，能够验证的等式是（ ）
“无字证明”（proofs without words），就是将数学命题用简单、有创意而且易于理解的几何图形来呈现．现将边长为a的正方形挖去一个边长为b的小正方形（a＞b）（如图甲），把剩下的部分拼成一个矩形（如图乙）．根据这两个图形中阴影部分的面积，能够验证的等式是（ ）| A． | a2-b2=（a+b）（a-b） | B． | （a-b）2=a2-2ab+b2 | ||
| C． | （a+2b）（a-b）=a2+ab-2b2 | D． | （a+b）2=a2+2ab+b2 |
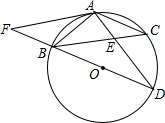如图，在⊙O中，弦AB=AC，BD为⊙O的直径，AD交BC于E，AF∥BC交DB的延长线于点F，AE=2，ED=4．