题目内容
11. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则由抛物线的特征可得到含a,b,c三个字母的等式或不等式为a-b+c>0.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则由抛物线的特征可得到含a,b,c三个字母的等式或不等式为a-b+c>0.
分析 根据二次函数y=ax2+bx+c(a≠0)的图象,可得x=-1时,y>0,所以a-b+c>0,据此解答即可,注意答案不唯一.
解答 解:根据二次函数y=ax2+bx+c(a≠0)的图象,可得
x=-1时,y>0,
∴a-b+c>0.
故答案为:a-b+c>0.(答案不唯一)
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$,则2xy的值是( )
| A. | 4 | B. | 2 | C. | -4 | D. | -2 |
17. “无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
 “无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+2b)(a-b)=a2+ab-2b2 | D. | (a+b)2=a2+2ab+b2 |
 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画三角形和平行四边形.
如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画三角形和平行四边形.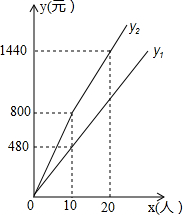 盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.