题目内容
16.已知等腰三角形ABC中,AD⊥BC于点D,且AD=$\frac{1}{2}$BC,则锐角∠C的度数为45°或75°或15°或30°.分析 (1)当∠C为底角时,分三种情况讨论,先根据题意分别画出图形,当AB=AC时,根据已知条件得出AD=BD=CD,从而得出△ABC底角的度数;当AB=BC时,先求出∠ABD的度数,再根据AB=BC,求出底角的度数;当AB=BC时,根据AD=$\frac{1}{2}$BC,AB=BC,得出∠DBA=30°,从而得出∠C的度数;
(2)当∠C为顶角时,根据等腰三角形的性质和直角三角形的性质即可得到结论.
解答  解:(1)当∠C为底角时,
解:(1)当∠C为底角时,
①如图1,当AB=AC时,
∵AD⊥BC,
∴BD=CD,
∵AD=$\frac{1}{2}$BC,
∴AD=BD=CD,
∴∠C=45°;
②如图2,当AB=BC时,
∵AD=$\frac{1}{2}$BC,
∴AD=$\frac{1}{2}$AB,
∴∠ABD=30°,
∴∠C=75°;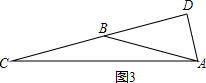
③如图3,当AB=BC时,
∵AD=$\frac{1}{2}$BC,AB=BC,
∴AD=$\frac{1}{2}$AB,
∴∠DBA=30°,
∴∠C=15°;
(2)当∠C为顶角时,
∵AD⊥BC,
∴∠ADC=90°,
∵AD=$\frac{1}{2}$BC,
∴AD=$\frac{1}{2}$AC,
∴∠C=30°,
∴∠C的度数为45°或75°或15°或30°;
故答案为:45°或75°或15°或30°.
点评 此题考查了含30度角的直角三角形和等腰三角形的性质,关键是根据题意画出图形,注意不要漏解.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
6.方程(m+2)x|m|+3mx+4=0是关于x的一元二次方程,则( )
| A. | m≠±2 | B. | m=±2 | C. | m=2 | D. | m=-2 |
11.已知二次函数y=ax2+bx+c自变量x与函数值y之间满足下列数量关系:
那么(a-b+c)( $\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$)的值为( )
| x | 0 | 2 | 3 |
| y | 0.37 | 0.37 | 4 |
| A. | 20 | B. | 8 | C. | 24 | D. | 4 |
5.方程x2=2x的根是( )
| A. | x=2 | B. | x=-2 | C. | x1=0,x2=-2 | D. | x1=0,x2=2 |
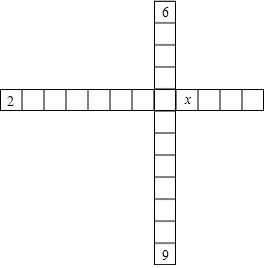 如图,横、竖各12个方格,每个方格都有一个数,已知横行上任意三个相邻数之和为10,竖列上任意三个相邻数之和为18,图中已填入2,6,9和x四个数,那么x代表的数是5.
如图,横、竖各12个方格,每个方格都有一个数,已知横行上任意三个相邻数之和为10,竖列上任意三个相邻数之和为18,图中已填入2,6,9和x四个数,那么x代表的数是5.