题目内容
11.已知二次函数y=ax2+bx+c自变量x与函数值y之间满足下列数量关系:| x | 0 | 2 | 3 |
| y | 0.37 | 0.37 | 4 |
| A. | 20 | B. | 8 | C. | 24 | D. | 4 |
分析 把x=0,y=0.37;x=2,y=0.37代入解析式得到b=-2a,则可确定抛物线的对称轴为直线x=1,利用抛物线的对称性得到x=-1时,y=4,即a-b+c=4,然后利用整体代入的方法计算(a-b+c)( $\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$)的值.
解答 解:∵x=0,y=0.37;x=2,y=0.37,
∴$\left\{\begin{array}{l}{c=0.37}\\{4a+2b+c=0.37}\end{array}\right.$,
∴4a+2b=0,解得b=-2a,
∴抛物线的对称轴为直线x=-$\frac{b}{2a}$=1,
∴x=-1与x=3时的函数值相等,
∴x=-1时,y=4,即a-b+c=4,
∴(a-b+c)( $\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$)=4×(-$\frac{b}{a}$)=4×(-$\frac{-2a}{a}$)=8,
故选B.
点评 本题考查了二次函数图形上点的坐标特征:利用抛物线上的点满足抛物线解析式,可判断点是否在抛物线上或确定点的坐标.

练习册系列答案
相关题目
2.下列事件中是必然事件的是( )
| A. | 任意掷一枚硬币,落地后正面和反面同时朝上 | |
| B. | 李阿姨申请了北京市小客车购买指标,在申请后的第一次“摇号”时就中签 | |
| C. | 分别从写有2、4、5三个数字的三张卡片中随机抽出一张,卡片上的数字一定能被2整除 | |
| D. | 哥哥的年龄比弟弟大. |
19.不等式组$\left\{\begin{array}{l}2-x≤0\\ 3x+2>-7\end{array}\right.$的解集是( )
| A. | -3<x≤2 | B. | -2<x≤3 | C. | x<-3或x≥2 | D. | x≥2 |
20.双曲线y=$\frac{k}{x}$位于第二、第四象限,则下面说法正确的是( )
| A. | y随x的增大而增大 | B. | y随x的增大而减小 | ||
| C. | k>0 | D. | k<0 |
1.石墨烯是世界上目前最薄却也最坚硬的纳米材料,还是导电性最好的材料,其理论厚度仅为0.00000000034米,该厚度用科学记数法表示为( )
| A. | 0.34×10-9米 | B. | 34.0×10-11米 | C. | 3.4×10-10米 | D. | 3.4×10-9米 |

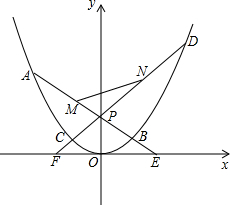 抛物线C0的顶点为原点O,且过点G(2,1).如图,过点P(0,2)分别作两条直线,l1:y=k1x+2和l2:y=k2x+2(其中k1•k2≠0),两直线分别与抛物线、x轴相交于点A、B、E和D、C、F,且M、N分别是AB、CD的中点.
抛物线C0的顶点为原点O,且过点G(2,1).如图,过点P(0,2)分别作两条直线,l1:y=k1x+2和l2:y=k2x+2(其中k1•k2≠0),两直线分别与抛物线、x轴相交于点A、B、E和D、C、F,且M、N分别是AB、CD的中点.