题目内容
1.某地区居民生活用电基本价格为每千瓦时0.40元,若每月用电量超过a千瓦时,则超过部分按基本电价的70%收费.(1)某户八月份用电84千瓦时,共交电费30.72元,求a.
(2)若该用户九月份的平均电费为0.36元,则九月份共用电多少千瓦?应交电费是多少元?
分析 (1)根据题中所给的关系,找到等量关系,共交电费是不变的,然后列出方程求出a;
(2)先设九月份共用电x千瓦时,从中找到等量关系,共交电费是不变的,然后列出方程求出.
解答 解:(1)由题意,得:
0.40a+(84-a)×0.40×70%=30.72,
解得:a=60;
(2)设九月份共用电x千瓦时,根据题意得:
0.40×60+(x-60)×0.40×70%=0.36x,
解得x=90,
所以0.36×90=32.40(元);
答:九月份共用电90千瓦时,应交电费32.40元.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
11.有一拦水坝横断面是一个等腰梯形,它的上底为6m,下底长为10m,高为2m,则此拦水坝的坡度与坡角分别为( )
| A. | 1:1,45° | B. | $\sqrt{3}$:1,30° | C. | $\sqrt{3}$:1,45° | D. | $\sqrt{3}$:1,60° |
12. 如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )
如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )
 如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )
如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )| A. | BD+DE=BC | B. | DE平分∠ADB | C. | AD平分∠EDC | D. | ED+AC>AD |
9.下列命题中,真命题是( )
| A. | 两条对角线互相垂直平分的四边形是矩形 | |
| B. | 有一条对角线平分一组对角的四边形是菱形 | |
| C. | 两条对角线相等的四边形是矩形 | |
| D. | 一组对边平行,一组对角相等的四边形是平行四边形 |
6.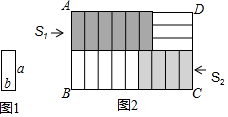 已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
 已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )| A. | 5b=2a | B. | 2b=a | C. | 3b=a | D. | 5b=3a |
13.以下列各组线段为边,能组成三角形的是( )
| A. | 3cm,5cm,8cm | B. | 8cm,7cm,13cm | C. | 13cm,12cm,31cm | D. | 7cm,7cm,15cm |
