题目内容
7.观察下面一列数:1,$\frac{3}{4}$,$\frac{5}{9}$,$\frac{7}{16}$,…则第n个数为$\frac{2n-1}{{n}^{2}}$(n为正整数).分析 设该数列第n个数为an,根据数列中数的变化找出变化规律“an=$\frac{2n-1}{{n}^{2}}$(n为正整数)”,依此规律即可得出结论.
解答 解:设该数列第n个数为an,
观察,发现规律:a1=1=$\frac{{1}^{2}-{0}^{2}}{{1}^{2}}$,a2=$\frac{3}{4}$=$\frac{{2}^{2}-{1}^{2}}{{2}^{2}}$,a3=$\frac{5}{9}$=$\frac{{3}^{2}-{2}^{2}}{{3}^{2}}$,a4=$\frac{7}{16}$=$\frac{{4}^{2}-{3}^{2}}{{4}^{2}}$,…,
∴an=$\frac{{n}^{2}-(n-1)^{2}}{{n}^{2}}$=$\frac{2n-1}{{n}^{2}}$(n为正整数).
故答案为:$\frac{2n-1}{{n}^{2}}$(n为正整数).
点评 本题考查了规律型中的数字的变化类,根据数列中数的变化找出变化规律“an=$\frac{2n-1}{{n}^{2}}$(n为正整数)”是解题的关键.

练习册系列答案
相关题目
2.下列事件中是必然事件的是( )
| A. | 任意掷一枚硬币,落地后正面和反面同时朝上 | |
| B. | 李阿姨申请了北京市小客车购买指标,在申请后的第一次“摇号”时就中签 | |
| C. | 分别从写有2、4、5三个数字的三张卡片中随机抽出一张,卡片上的数字一定能被2整除 | |
| D. | 哥哥的年龄比弟弟大. |
12. 如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )
如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )
 如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )
如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )| A. | BD+DE=BC | B. | DE平分∠ADB | C. | AD平分∠EDC | D. | ED+AC>AD |
19.不等式组$\left\{\begin{array}{l}2-x≤0\\ 3x+2>-7\end{array}\right.$的解集是( )
| A. | -3<x≤2 | B. | -2<x≤3 | C. | x<-3或x≥2 | D. | x≥2 |

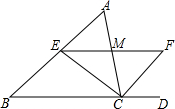 如图,△ABC中,CE、CF分别是∠ACB及外角∠ACD的平分线,且CE交AB于点E,EF交AC于点M,已知EF∥BC.
如图,△ABC中,CE、CF分别是∠ACB及外角∠ACD的平分线,且CE交AB于点E,EF交AC于点M,已知EF∥BC.