题目内容
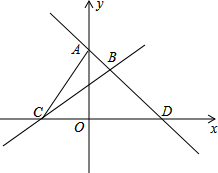 如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(-2,0),且与直线AD交于点B,且点B的横坐标为a.
如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(-2,0),且与直线AD交于点B,且点B的横坐标为a.(1)当a=1时,求直线BC的解析式;
(2)在(1)的条件下,请直接写出k1x+b1>k2x+b2时,对应的x的取值范围;
(3)设△ABC的面积为S,用含a的代数式表示S,并求出当直线CB把△ACD的面积分为1:2的两部分时,对应a的值.
考点:一次函数综合题
专题:
分析:(1)先求出直线AD的解析式,再求得B点的纵坐标,再代入求得直线BC的解析式;
(2)根据一次函数的增减性,并结合函数图象可以求得不等式的解集;
(3)分三种情况分别求出△ABC的面积函数关系式.
(2)根据一次函数的增减性,并结合函数图象可以求得不等式的解集;
(3)分三种情况分别求出△ABC的面积函数关系式.
解答:解:(1)由题意得:直线AD过点A(0,4),D(4,0),
∴
解得:
.
∴直线AD的解析式为y1=-x+4
又因为点B在AD上,且B点的横坐标为a=1,所以纵坐标为3,即B(1,3)
由题意的直线BC过点B(1,3),C(-2,0)
∴
解得:
.
∴直线BC的解析式为y2=x+2
(2)因为直线AD与直线BC相交于点B(1,3)
由图象得:k1x+b1>k2x+b2时x的取值范围为x<1.
(3)△ABC的面积计算有三种形式,分别为点B在点A上方、在AD中间、在点D下方.
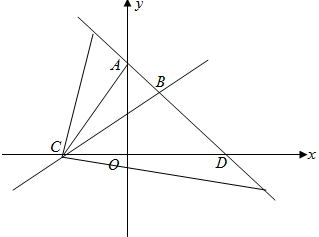
①点B在点A上方,即a≤0时:S△ABC=S△BCO+S△BAO-S△ACO
∴S=
×2×(-a+4)+
×4×(-a)-
×2×4=-3a
②当点B在点A和点D中间,即0<a<4时,:S△ABC=S△ACD-S△BCD
∴S=
×6×4-
×6×(-a+4)=3a
③当点B在点D下方,即a≥4时,:S△ABC=S△ACD+S△BCD
∴S=
×6×4+
×6×(-(-a+4))=3a
综上所述得:S=
当直线CB把△ACD的面积分为1:2两部分时,即B点在点A和点D中间时.
此时S△ABC=3a,S△ACD=12.
当S△ABC:S△ACD=1:3时,即3a:12=1:3,∴a=
;
当S△ABC:S△ACD=2:3时,即3a:12=2:3,∴a=
.
∴
|
|
∴直线AD的解析式为y1=-x+4
又因为点B在AD上,且B点的横坐标为a=1,所以纵坐标为3,即B(1,3)
由题意的直线BC过点B(1,3),C(-2,0)
∴
|
|
∴直线BC的解析式为y2=x+2
(2)因为直线AD与直线BC相交于点B(1,3)
由图象得:k1x+b1>k2x+b2时x的取值范围为x<1.
(3)△ABC的面积计算有三种形式,分别为点B在点A上方、在AD中间、在点D下方.

①点B在点A上方,即a≤0时:S△ABC=S△BCO+S△BAO-S△ACO
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②当点B在点A和点D中间,即0<a<4时,:S△ABC=S△ACD-S△BCD
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
③当点B在点D下方,即a≥4时,:S△ABC=S△ACD+S△BCD
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
综上所述得:S=
|
当直线CB把△ACD的面积分为1:2两部分时,即B点在点A和点D中间时.
此时S△ABC=3a,S△ACD=12.
当S△ABC:S△ACD=1:3时,即3a:12=1:3,∴a=
| 4 |
| 3 |
当S△ABC:S△ACD=2:3时,即3a:12=2:3,∴a=
| 8 |
| 3 |
点评:本题是一次函数的综合应用.综合性较强,注意第(3)题分三种情况分别求出△ABC的面积函数关系式.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
一个数的算术平方根是a,则比这个数大2的数是( )
| A、a2+2 | ||
B、
| ||
C、
| ||
| D、a+2 |
 如图,某公园内有一棵大树,为测量树高,小明C处用侧角仪测得∠ADE=30°,量出DC=2m,BC=30m,请帮助小明计算出树高AB.
如图,某公园内有一棵大树,为测量树高,小明C处用侧角仪测得∠ADE=30°,量出DC=2m,BC=30m,请帮助小明计算出树高AB.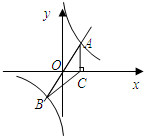 如图,直线y=x与反比例函数
如图,直线y=x与反比例函数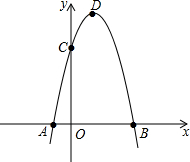 如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D
如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D
 如图,直线a∥b,∠3-∠2=∠2-∠1=d°>0.其中∠3<90°,∠1=50°.求∠4度数最大可能的整数值.
如图,直线a∥b,∠3-∠2=∠2-∠1=d°>0.其中∠3<90°,∠1=50°.求∠4度数最大可能的整数值.