题目内容
如图，某公园内有一棵大树，为测量树高，小明C处用侧角仪测得∠ADE=30°，量出DC=2m，BC=30m，请帮助小明计算出树高AB．考点：勾股定理的应用
专题：
分析：此题可由D处用测角仪测得树顶端A的仰角为30°的正切值及BC的长求得AE的长，再加上测角仪高DC求得．
解答：解：∵在D处用测角仪测得树顶端A的仰角为30°，
∴∠ADE=30°，ED=CB=30cm，
∴AE=DE•tan30°=30×
=10
，
∵DC=2m，
则树高AB=AE+EB=AE+DC=（10
+2）m．
答：树高AB约为（10
+2）米．
∴∠ADE=30°，ED=CB=30cm，
∴AE=DE•tan30°=30×
| ||
| 3 |
| 3 |
∵DC=2m，
则树高AB=AE+EB=AE+DC=（10
| 3 |
答：树高AB约为（10
| 3 |
点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．
练习册系列答案
相关题目
如果不等式组
有解，那么m的取值范围是（ ）
|
| A、m＞1 | B、m≤2 |
| C、1＜m≤2 | D、m＞-2 |
下列等式正确的是（ ）
| A、（-x2）3=-x5 |
| B、x8÷x4=x4 |
| C、（-a+b）2=a2+2ab+b2 |
| D、（2xy）3=2x3y3 |
如图，几何体的俯视图是（ ）
A、 |
B、 |
C、 |
D、 |
已知（x-1）2=25，则x的值为（ ）
| A、6 | B、4 | C、-4 | D、-4或6 |
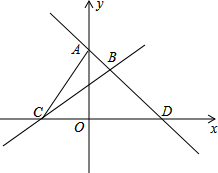如图，直线AD：y1=k1x+b1过点A（0，4），D（4，0），直线BC：y2=k2x+b2过点C（-2，0），且与直线AD交于点B，且点B的横坐标为a．
如图，⊙O是△ABC的外接圆，点D在⊙O上，连接BD、CD，且∠ACB=∠BDC=60°，