题目内容
 如图,直线a∥b,∠3-∠2=∠2-∠1=d°>0.其中∠3<90°,∠1=50°.求∠4度数最大可能的整数值.
如图,直线a∥b,∠3-∠2=∠2-∠1=d°>0.其中∠3<90°,∠1=50°.求∠4度数最大可能的整数值.考点:平行线的性质
专题:
分析:根据平行线的性质和三角形外角性质求出∠4-∠3=∠3-∠2,根据已知求出∠3=
,根据∠3<90°求出∠4的范围,即可得出答案.
| 2∠4+50° |
| 3 |
解答:解: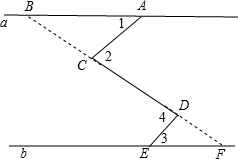
延长CD交直线b于F,延长DC交直线a于B,
∵直线a∥直线b,
∴∠ABC=∠DFE,
∵∠ABC=∠2-∠1,∠DFE=∠4-∠3,
∴∠4-∠3=∠3-∠2,
∴∠4=2∠3-∠2,
又∵∠3-∠2=∠2-∠1,∠1=50°,
∴2∠2=∠3+50°,
∴2∠4=4∠3-2∠2=4∠3-∠3-50°=3∠3-50°,
∴∠3=
,
而∠3<90°,
∴
<90°,
∴∠4<110°,
∴∠4的最大可能的整数值是109°.

延长CD交直线b于F,延长DC交直线a于B,
∵直线a∥直线b,
∴∠ABC=∠DFE,
∵∠ABC=∠2-∠1,∠DFE=∠4-∠3,
∴∠4-∠3=∠3-∠2,
∴∠4=2∠3-∠2,
又∵∠3-∠2=∠2-∠1,∠1=50°,
∴2∠2=∠3+50°,
∴2∠4=4∠3-2∠2=4∠3-∠3-50°=3∠3-50°,
∴∠3=
| 2∠4+50° |
| 3 |
而∠3<90°,
∴
| 2∠4+50° |
| 3 |
∴∠4<110°,
∴∠4的最大可能的整数值是109°.
点评:本题考查了平行线的性质,三角形外角性质的应用,解此题的关键是求出∠AOE和∠A的度数,题目比较好,难度适中.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
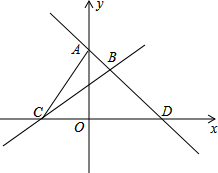 如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(-2,0),且与直线AD交于点B,且点B的横坐标为a.
如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(-2,0),且与直线AD交于点B,且点B的横坐标为a. 如图,⊙O是△ABC的外接圆,点D在⊙O上,连接BD、CD,且∠ACB=∠BDC=60°,
如图,⊙O是△ABC的外接圆,点D在⊙O上,连接BD、CD,且∠ACB=∠BDC=60°, 如图,将菱形ABCD放在直角坐标中,使得点B与原点重合,对角线BD在x轴上,点A恰好在反比例函数y=
如图,将菱形ABCD放在直角坐标中,使得点B与原点重合,对角线BD在x轴上,点A恰好在反比例函数y=