题目内容
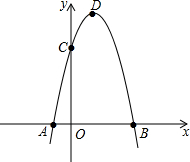 如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D
如图,抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),与Y相交于点C顶点为D(1)直接写出ABC点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P线段BC一个动点,过点P作PF∥DE交抛物线于点F,设点P横坐标为m
①用含m代数式表示线段PF,并求出当m何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S关于m的函数关系式,并求出当m取何值时,S有最大值,最大值是多少.
考点:二次函数综合题
专题:
分析:(1)已知了抛物线的解析式,当y=0时可求出A,B两点的坐标,当x=0时,可求出C点的坐标.根据对称轴x=-
可得出对称轴的解析式.
(2)①PF的长就是当x=m时,抛物线的值与直线BC所在一次函数的值的差.可先根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,然后根据坐标系中两点的距离公式,可求出DE的长,然后让PF=DE,即可求出此时m的值.
②可将三角形BCF分成两部分来求:一部分是三角形PFC,以PF为底边,以P的横坐标为高即可得出三角形PFC的面积.一部分是三角形PFB,以PF为底边,以P、B两点的横坐标差的绝对值为高,即可求出三角形PFB的面积.然后根据三角形BCF的面积=三角形PFC的面积+三角形PFB的面积,可求出关于S、m的函数关系式,由此可求出S的最大值.
| b |
| 2a |
(2)①PF的长就是当x=m时,抛物线的值与直线BC所在一次函数的值的差.可先根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,然后根据坐标系中两点的距离公式,可求出DE的长,然后让PF=DE,即可求出此时m的值.
②可将三角形BCF分成两部分来求:一部分是三角形PFC,以PF为底边,以P的横坐标为高即可得出三角形PFC的面积.一部分是三角形PFB,以PF为底边,以P、B两点的横坐标差的绝对值为高,即可求出三角形PFB的面积.然后根据三角形BCF的面积=三角形PFC的面积+三角形PFB的面积,可求出关于S、m的函数关系式,由此可求出S的最大值.
解答:解:(1)设0=-x2+2x+3,
解得:x=-1或3,
∵抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),
∴A(-1,0),B(3,0),
∵抛物线与y轴相交于点C,
∴C(0,3),
∴抛物线的对称轴是:直线x=1.
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:
,
解得:k=-1,b=3.
所以直线BC的函数关系式为:y=-x+3.
当x=1时,y=-1+3=2,
∴E(1,2).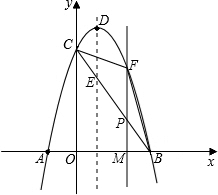
当x=m时,y=-m+3,
∴P(m,-m+3).
在y=-x2+2x+3中,当x=1时,y=4.
∴D(1,4).
当x=m时,y=-m2+2m+3,
∴F(m,-m2+2m+3).
∴线段DE=4-2=2,线段PF=-m2+2m+3-(-m+3)=-m2+3m.
∵PF∥DE,
ED时,四边形PEDF为平行四边形.
由-m2+3m=2,解得:m1=2,m2=1(不合题意,舍去).
因此,当m=2时,四边形PEDF为平行四边形.
②设直线PF X点M由B(3,0),O(0,0),
可得:OB=OM+MB=3.
∵S=S△BPF+S△CPF.
∴S=
PF×BM+
PF×OM=
PF×(BM+OM)=
PF×OB
∵S=
×3(-m2+3m)=-
m2+
m(0≤m≤3).
∵S=-
(m-
)2+
∴当m=
,S最大值=
.
解得:x=-1或3,
∵抛物线y=-x2+2x+3与x相交于AB(点A点B左侧),
∴A(-1,0),B(3,0),
∵抛物线与y轴相交于点C,
∴C(0,3),
∴抛物线的对称轴是:直线x=1.
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:
|
解得:k=-1,b=3.
所以直线BC的函数关系式为:y=-x+3.
当x=1时,y=-1+3=2,
∴E(1,2).

当x=m时,y=-m+3,
∴P(m,-m+3).
在y=-x2+2x+3中,当x=1时,y=4.
∴D(1,4).
当x=m时,y=-m2+2m+3,
∴F(m,-m2+2m+3).
∴线段DE=4-2=2,线段PF=-m2+2m+3-(-m+3)=-m2+3m.
∵PF∥DE,
ED时,四边形PEDF为平行四边形.
由-m2+3m=2,解得:m1=2,m2=1(不合题意,舍去).
因此,当m=2时,四边形PEDF为平行四边形.
②设直线PF X点M由B(3,0),O(0,0),
可得:OB=OM+MB=3.
∵S=S△BPF+S△CPF.
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S=
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
∵S=-
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
∴当m=
| 3 |
| 2 |
| 27 |
| 8 |
点评:本题主要考查了二次函数的综合应用,根据二次函数得出相关点的坐标和对称轴的解析式是解题的基础,其中用到的知识点有平行四边形的判定和性质、解一元二次方程、用待定系数法确定一次函数的解析式,三角形面积公式的运用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
下列等式正确的是( )
| A、(-x2)3=-x5 |
| B、x8÷x4=x4 |
| C、(-a+b)2=a2+2ab+b2 |
| D、(2xy)3=2x3y3 |
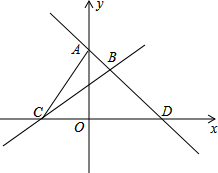 如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(-2,0),且与直线AD交于点B,且点B的横坐标为a.
如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(-2,0),且与直线AD交于点B,且点B的横坐标为a. 如图,正方形纸片ABCD的边长AB=12,E是DC上一点CE=5,折叠正方形纸片,使点B和点E重合,折痕为FG,试求GF的长.
如图,正方形纸片ABCD的边长AB=12,E是DC上一点CE=5,折叠正方形纸片,使点B和点E重合,折痕为FG,试求GF的长. 如图,⊙O是△ABC的外接圆,点D在⊙O上,连接BD、CD,且∠ACB=∠BDC=60°,
如图,⊙O是△ABC的外接圆,点D在⊙O上,连接BD、CD,且∠ACB=∠BDC=60°,