题目内容
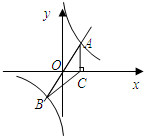 如图,直线y=x与反比例函数y=
如图,直线y=x与反比例函数y=| k |
| x |
(1)求反比例函数的表达式.
(2)求△ABC的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A的坐标代入y=x即可求得a的值,然后代入反比例函数解析式即可求得k的值,从而求得函数的解析式;
(2)根据A、B的坐标,即可求得AC的长,和AC边上的高,利用三角形面积公式即可求解.
(2)根据A、B的坐标,即可求得AC的长,和AC边上的高,利用三角形面积公式即可求解.
解答:解:(1)把A(a,3)代入y=x,得x=a=3,
则A的坐标是(3,3),
同理B的坐标是(-3,-3).
把A(3,3)代入y=
得:k=9,
则反比例函数的解析式是:y=
.
(2)∵A的坐标是(3,3),B的坐标是(-3,-3).
∴AC=3,AC边上的高是6,
则S△ABC=
×3×6=9.
则A的坐标是(3,3),
同理B的坐标是(-3,-3).
把A(3,3)代入y=
| k |
| x |
则反比例函数的解析式是:y=
| 9 |
| x |
(2)∵A的坐标是(3,3),B的坐标是(-3,-3).
∴AC=3,AC边上的高是6,
则S△ABC=
| 1 |
| 2 |
点评:本题考查了待定系数法求函数的解析式,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
相关题目
下列说法错误的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知(x-1)2=25,则x的值为( )
| A、6 | B、4 | C、-4 | D、-4或6 |
 如图,已知:AD∥BC,AD=CB,AE=CF,
如图,已知:AD∥BC,AD=CB,AE=CF,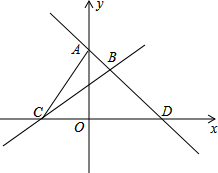 如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(-2,0),且与直线AD交于点B,且点B的横坐标为a.
如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(-2,0),且与直线AD交于点B,且点B的横坐标为a. 如图,正方形纸片ABCD的边长AB=12,E是DC上一点CE=5,折叠正方形纸片,使点B和点E重合,折痕为FG,试求GF的长.
如图,正方形纸片ABCD的边长AB=12,E是DC上一点CE=5,折叠正方形纸片,使点B和点E重合,折痕为FG,试求GF的长.