Question

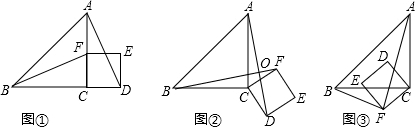
如图①，等腰Rt△ABC中，∠ACB=90°，F是AC边上一点（点F与A、C不重合），以CF为边在△ABC外作正方形CDEG，连接BF、AD，则有结论：BF=AD，BF⊥AD．

问题解决：
将图①中的正方形CDEF绕点C按顺时针方向旋转角度α（0°＜α＜360°），得如图②、图③的情形．
（1）若图②中BF交AD于点O，试判断：BF=AD，BF⊥AD是否仍然成立，并结合图②证明你的判断；
（2）在正方形CDEF绕点C按顺时针方向旋转过程中，以A、C、F为顶点的三角形与△BCF能否全等？若能，直接写出旋转角α的值；若不能，请说明理由．

Answer 1

考点：全等三角形的判定与性质,正方形的性质,旋转的性质

专题：

分析：（1）①证△BCF≌△ACD推出∠CAD=∠FBC，BF=AD，即可得出结论；②证△BCF≌△ACD推出∠CAD=∠FBC，BF=AD，即可得出结论；
（2）如图4，当△ACF≌△BCF时，就可以得出∠ACF=∠BCF，由∠ACB=90°据可以得出a的值，如图5，当△ACF≌△BCF时，就可以得出∠ACF=∠BCF，由∠ACB=90°据可以得出∠ACF的值而得出a的值．

解答：解：（1）BF=AD，BF⊥AD仍然成立，
理由：如图②∵△ABC是等腰直角三角形，∠ACB=90°，
∴AC=BC，
∵四边形CDEF是正方形，
∴CD=CF，∠FCD=90°，
∴∠ACB+∠ACF=∠FCD+∠ACF，
∴∠BCF=∠ACD，
在△BCF和△ACD中

BC=AC ∠BCF=∠ACD CF=CD

，
∴△BCF≌△ACD（SAS），
∴BF=AD，∠CBF=∠CAD，
∵∠BHC=∠AHO，∠CBH+∠BHC=90°，
∴∠CAD+∠AHO=90°，
∴∠AOH=90°，
∴BF⊥AD；
（2）如图4，当△ACF≌△BCF时，
∴∠ACF=∠BCF

点评：本题考查了正方形性质，全等三角形的性质和判定，勾股定理等知识点的应用，关键是推出△BCF≌△ACD，主要考查学生运用定理进行推理和计算的能力，有一定的难度．