题目内容
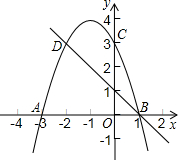 如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于点C.C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于点C.C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)求二次函数的表达式;
(2)根据图象写出使一次函数值大于二次函数值的x的取值范围.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式,二次函数与不等式(组)
专题:
分析:(1)根据函数图象设抛物线的解析式为y=a(x+3)(x-1),由待定系数法求出其解即可.
(2)根据函数图象设直线的解析式为y=kx+b,由直线经过(0,1)和(1,0)由待定系数法求出解析式,再与二次函数的解析式构成方程组求出其解就可以求出一次函数与二次函数的交点坐标,由函数图象就可以求出结论.
(2)根据函数图象设直线的解析式为y=kx+b,由直线经过(0,1)和(1,0)由待定系数法求出解析式,再与二次函数的解析式构成方程组求出其解就可以求出一次函数与二次函数的交点坐标,由函数图象就可以求出结论.
解答:解:(1)设抛物线的解析式为y=a(x+3)(x-1),由函数图象,得
3=a(0+3)(0-1),
解得:a=-1,
y=-(x+3)(x-1),
y=-x2-2x+3.
∴二次函数的表达式为:y=-x2-2x+3;
(2)设直线的解析式为y=kx+b,由直线经过(0,1)和(1,0),得
,
解得:
,
一次函数的解析式为:y=-x+1.
,
解得:
,
,
故抛物线与x轴的加点坐标为:(-2,3)或(1,0).
由函数图象得:当x<-2或x>1时,一次函数值大于二次函数值.
3=a(0+3)(0-1),
解得:a=-1,
y=-(x+3)(x-1),
y=-x2-2x+3.
∴二次函数的表达式为:y=-x2-2x+3;
(2)设直线的解析式为y=kx+b,由直线经过(0,1)和(1,0),得
|
解得:
|
一次函数的解析式为:y=-x+1.
|
解得:
|
|
故抛物线与x轴的加点坐标为:(-2,3)或(1,0).
由函数图象得:当x<-2或x>1时,一次函数值大于二次函数值.
点评:本题考查了待定系数法求一次函数的解析式和二次函数的解析式的运用,二元二次方程组的解法的运用,抛物线与x轴的交点坐标的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
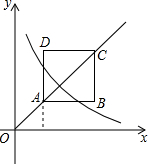 如图,正方形ABCD位于第一象限,AC=2
如图,正方形ABCD位于第一象限,AC=2| 2 |
| k |
| x |
| A、0<k≤1或k≥6 |
| B、1≤k≤6 |
| C、1≤k≤9 |
| D、0<k≤1或k≥9 |
 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,求证:
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,求证: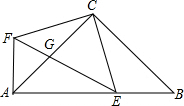 如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF.
如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF. 如图,在△ABC中,M为AC中点,连接BM,点D为BM上的一点,过点C作CE∥BM,过点D作DE∥AB,CE、DE交于点E,连接BE,求证:BE=AD.
如图,在△ABC中,M为AC中点,连接BM,点D为BM上的一点,过点C作CE∥BM,过点D作DE∥AB,CE、DE交于点E,连接BE,求证:BE=AD.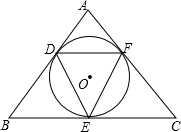 如图,⊙O是△ABC的内切圆,D、E、F是切点,D、E、F分别在AB、BC、CA上.问:△DEF的形状有什么特点?
如图,⊙O是△ABC的内切圆,D、E、F是切点,D、E、F分别在AB、BC、CA上.问:△DEF的形状有什么特点?