题目内容
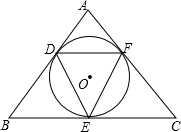 如图,⊙O是△ABC的内切圆,D、E、F是切点,D、E、F分别在AB、BC、CA上.问:△DEF的形状有什么特点?
如图,⊙O是△ABC的内切圆,D、E、F是切点,D、E、F分别在AB、BC、CA上.问:△DEF的形状有什么特点?考点:三角形的内切圆与内心
专题:
分析:首先运用切线的性质证明∠ADF=∠AFD,然后运用三角形的内角和定理证明∠DEF为锐角即可解决问题.
解答:解:∵⊙O是△ABC的内切圆,
∴AD=AF,∠ADF=∠DEF;
∴∠ADF=∠AFD(设为α);
∵2α+∠A=180°,
∴α=90°-
∠A,
∴∠DEF=α为锐角;
同理可求∠EDF、∠DFE均为锐角,
∴△DEF为锐角三角形.
∴AD=AF,∠ADF=∠DEF;
∴∠ADF=∠AFD(设为α);
∵2α+∠A=180°,
∴α=90°-
| 1 |
| 2 |
∴∠DEF=α为锐角;
同理可求∠EDF、∠DFE均为锐角,
∴△DEF为锐角三角形.
点评:该命题在考查三角形的内切圆及其圆心的性质的同时,还考查了三角形的内角和定理及其应用问题;解题的关键是灵活运用有关定理来解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下面是按规律排列的一列数:1、-2、4、-8、16、…其中第7个与第8个数分别为( )
| A、-32,64 |
| B、23,-64 |
| C、-64,128 |
| D、64,-128 |
 如图,EA∥DF,AE=DF,要使△ACE≌△DBF,则只要( )
如图,EA∥DF,AE=DF,要使△ACE≌△DBF,则只要( )| A、AB=CD |
| B、EC=BF |
| C、∠A=∠D |
| D、AB=BC |
在矩形ABCD中对角线AC,BD相交于点O,∠AOB=60°,AC=10cm,则AB的长为( )
| A、3cm | B、4cm |
| C、5cm | D、10cm |
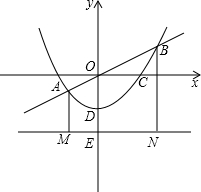 对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(-1,n),请完成下列任务:
对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(-1,n),请完成下列任务: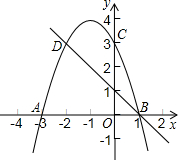 如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于点C.C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于点C.C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.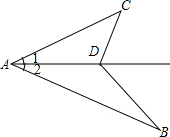 如图,AB>AC,∠1=∠2,求证:AB-AC>BD-CD.
如图,AB>AC,∠1=∠2,求证:AB-AC>BD-CD.