题目内容
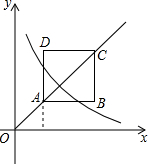 如图,正方形ABCD位于第一象限,AC=2
如图,正方形ABCD位于第一象限,AC=2| 2 |
| k |
| x |
| A、0<k≤1或k≥6 |
| B、1≤k≤6 |
| C、1≤k≤9 |
| D、0<k≤1或k≥9 |
考点:反比例函数与一次函数的交点问题
专题:
分析:先根据题意求出A点的坐标,再根据AC=2
,求得AB=AC=2,AB、BC分别平行于x轴、y轴求出B、C两点的坐标,再根据双曲线y=
(k≠0)分别经过A、C两点时k的取值范围即可.
| 2 |
| k |
| x |
解答:解:点A在直线y=x上,其中A点的横坐标为1,则把x=1代入y=x解得y=1,则A的坐标是(1,1),
∵AC=2
,
∴AB=BC=2,
∴C点的坐标是(3,3),
∴当双曲线y=
经过点(1,1)时,k=1;
当双曲线y=
经过点(3,3)时,k=9,
因而1≤k≤9.
故选:C.
∵AC=2
| 2 |
∴AB=BC=2,
∴C点的坐标是(3,3),
∴当双曲线y=
| k |
| x |
当双曲线y=
| k |
| x |
因而1≤k≤9.
故选:C.
点评:本题主要考查了反比例函数,用待定系数法求一次函数的解析式,解此题的关键是理解题意进而求出k的值.

练习册系列答案
相关题目
如图是一个简单的数值运算程序,当输入的x的值为2时,则输出的值为( )


| A、-4 | B、4 | C、5 | D、-8 |
下面是按规律排列的一列数:1、-2、4、-8、16、…其中第7个与第8个数分别为( )
| A、-32,64 |
| B、23,-64 |
| C、-64,128 |
| D、64,-128 |
数轴上的点A到-2的距离是6,则点A表示的数为( )
| A、4或-8 | B、4 |
| C、-8 | D、6或-6 |
 如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.
如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.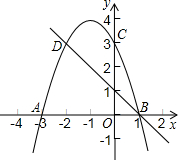 如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于点C.C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A、B两点,与y轴相交于点C.C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.