题目内容
1.已知a,b是△ABC的两边,且$\sqrt{a-3}$+b2+4=4b,若第三边c是奇数,则此三角形的周长为8.分析 根据非负数的性质确定a、b的值,然后利用三角形的三边关系确定c的值,从而求得三角形的周长.
解答 解:由且$\sqrt{a-3}$+b2+4=4b得:且$\sqrt{a-3}$+(b-2)2=0,
所以a=3,b=2,
根据三角形的三边关系得:1<c<5,
∵c为奇数,
∴c=3,
∴周长为3+2+3=8,
故答案为:8.
点评 本题考查了三角形的三边关系,解题的关键是能够根据非负数的性质确定第三边的长,难度不大.

练习册系列答案
相关题目
12.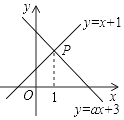 如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是( )
如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是( )
 如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是( )
如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ |
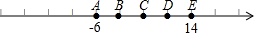 如图,A、B、C、D、E是未标出原点的数轴上的五个点,点A和点E对应的数位-6和14,且AB=BC=CD=DE,则点D所表示的数是( )
如图,A、B、C、D、E是未标出原点的数轴上的五个点,点A和点E对应的数位-6和14,且AB=BC=CD=DE,则点D所表示的数是( )
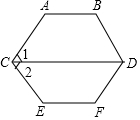 如图,AB∥CD.CD∥EF.∠1=∠2=60°.,求∠A和∠E的度数.它们相等吗?
如图,AB∥CD.CD∥EF.∠1=∠2=60°.,求∠A和∠E的度数.它们相等吗?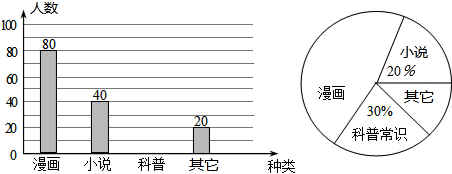
 如图,将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2 ②∠3=∠4 ③∠4+∠5=180° ④∠2+∠3=90°
如图,将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2 ②∠3=∠4 ③∠4+∠5=180° ④∠2+∠3=90°