题目内容
6.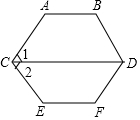 如图,AB∥CD.CD∥EF.∠1=∠2=60°.,求∠A和∠E的度数.它们相等吗?
如图,AB∥CD.CD∥EF.∠1=∠2=60°.,求∠A和∠E的度数.它们相等吗?解:∵AB∥CD(已知)
∴∠A=180°-∠1
=180°-60°
=120°.
(两直线平行,同旁内角互补)
∵CD∥EF(已知)
∴∠E=180°-∠2=180°-60°=120°
∴∠A=∠E.
分析 先根据AB∥CD得出∠A的度数,再由CD∥EF求出∠E的度数,进而可得出结论.
解答 解:∵AB∥CD(已知)
∴∠A=180°-∠1
=180°-60°
=120°(两直线平行,同旁内角互补).
∵CD∥EF(已知),
∴∠E=180°-∠2=180°-60°=120°
∴∠A=∠E.
故答案为:1,120°,两直线平行,同旁内角互补,CD,EF,180°,2,180,60,120,=.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,O为坐标原点.若OB=OC=$\frac{1}{2}$OA,则b的值为 ( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | -1 |
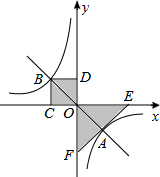 如图,过点O作直线与双曲线y=$\frac{k}{x}$(k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴、y轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1,S2的数量关系是2S1=S2.
如图,过点O作直线与双曲线y=$\frac{k}{x}$(k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴、y轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1,S2的数量关系是2S1=S2. 用五个完全相同的小正方体组成如图所示的立体图形,从上面看到的图形是( )
用五个完全相同的小正方体组成如图所示的立体图形,从上面看到的图形是( )


