题目内容
12.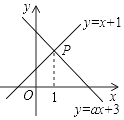 如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是( )
如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ |
分析 先把x=1代入y=x+1,得出y=2,则两个一次函数的交点P的坐标为(1,2);那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
解答 解:把x=1代入y=x+1,得出y=2,
函数y=x+1和y=ax+3的图象交于点P(1,2),
即x=1,y=2同时满足两个一次函数的解析式.
所以关于x,y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
故选:A.
点评 此题考查了一次函数与二元一次方程组的联系,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的一次函数式,因此方程组的解就是两个相应的一次函数图象的交点坐标.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
3.下列说法正确的是( )
| A. | -$\frac{5}{3}$的倒数是$\frac{5}{3}$ | B. | -$\frac{2{x}^{2}y}{3}$的系数是$\frac{2}{3}$ | ||
| C. | -32的值是9 | D. | 3n-4m2n是三次二项式 |
17.抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,O为坐标原点.若OB=OC=$\frac{1}{2}$OA,则b的值为 ( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | -1 |
4.二次函数y=(x+3)2+7的顶点坐标是( )
| A. | (-3,7) | B. | (3,7) | C. | (-3,-7) | D. | (3,-7) |
 某电信公司有甲、乙两种手机收费业务,仅上网流量收费不同,图中I1、I2分别表示甲、乙两种业务每月流量费用y(元)与上网流量x(GB)的之间的函数关系.
某电信公司有甲、乙两种手机收费业务,仅上网流量收费不同,图中I1、I2分别表示甲、乙两种业务每月流量费用y(元)与上网流量x(GB)的之间的函数关系. 如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移$\sqrt{2}$个单位,则平移后直线的解析式为y=2x.
如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移$\sqrt{2}$个单位,则平移后直线的解析式为y=2x.