题目内容
12.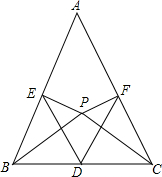 在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.
在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.(1)说明BP=CP;
(2)说明DE=DF.
分析 (1)根据等腰三角形的性质得到∠ABC=∠ACB,由角的和差得到∠PBC=∠PCB,即可得到结论;
(2)由PE⊥AC于点E,PF⊥AB于点F,得到∠PEB=∠PFC=90°,证得△BEP≌△CFP,根据全等三角形的性质即可得到结论.
解答 证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABP=∠ACP,
∴∠PBC=∠PCB,
∴PB=PC;
(2)∵PE⊥AC于点E,PF⊥AB于点F,
∴∠PEB=∠PFC=90°,
在△BEP与△CFP中,
$\left\{\begin{array}{l}{∠PEB=∠PFC}\\{∠PBE=∠PCF}\\{PB=PC}\end{array}\right.$,
∴△BEP≌△CFP,
∴PE=PF.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质和判定,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
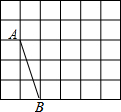 在如图所示的5×6方格中(每个方格的边长为1),点A、B在格点上.
在如图所示的5×6方格中(每个方格的边长为1),点A、B在格点上.
 A,B,C在一条直线上,△ABE与△BCD为等边三角形,AD与CE交于H,
A,B,C在一条直线上,△ABE与△BCD为等边三角形,AD与CE交于H,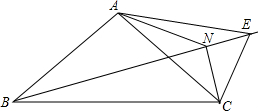 如图,在△ABC中,AB=AC,∠ABC=α.过点B作一直线l,在l上取点E,使AE=AC,连接CE.∠CAE的平分线交BE于点N,连接NC.
如图,在△ABC中,AB=AC,∠ABC=α.过点B作一直线l,在l上取点E,使AE=AC,连接CE.∠CAE的平分线交BE于点N,连接NC.