题目内容
20.四边形ABDC中,AB∥CD,∠BAC=90°,AB=AC,BE⊥AD交AC于E.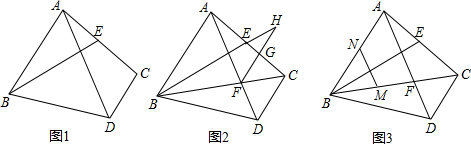
(1)求证:AE=CD;
(2)点G是AC上一点,若CG=AE,BE、FG的延长线交于点H,求证:EH=GH;
(3)点M在BC上,且BM=CF,MN∥AD,若AE=2,求BN的值.
分析 (1)根据四边形ABDC中,AB∥CD,∠BAC=90°,AB=AC,BE⊥AD,可以得到∠BAE=∠C,∠EBA=∠DAC,从而可以得到△EBA≌△DAC,进而得到AE=CD;
(2)要证EH=GH,只要证∠HGE=∠HEG即可,要证∠HGE=∠HEG,只要证∠AEB=∠CGF,根据题意和第一问中结论可以求出所求的结论成立,从而解答问题;
(3)由AE=2,可得CD=2,然后根据题意可以证CD=BN,从而可以求得BN的长.
解答 (1)证明:如下图1所示,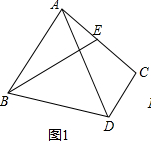
∵AB∥CD,∠BAC=90°,
∴∠BAC+∠C=180°,∠EBA+∠AEB=90°.
∴∠C=90.
∵BE⊥AD,
∴∠DAC+∠AEB=90°.
∴∠EBA=∠DAC.
在△EBA和△DAC中,
$\left\{\begin{array}{l}{∠EBA=∠DAC}\\{AB=AC}\\{∠BAC=∠C}\end{array}\right.$,
∴△EBA≌△DAC(ASA).
∴AE=CD.
(2)证明:如下图2所示,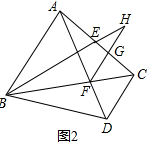
∵AB=AC,∠BAC=90°,
∴∠ACB=45°.
又∵∠ACD=90°,
∴∠GCF=∠DCF=45°.
∵AE=CD,CG=AE,
∴CG=CD.
在△CFG和△CFD中
$\left\{\begin{array}{l}{CG=CD}\\{∠GCF=∠DCF}\\{CF=CF}\end{array}\right.$
∴△CFG≌△CDF(SAS).
∴∠CGF=∠CDF.
∵∠CGF=∠HGE,∠HEG=∠AEB,∠AEB+∠CAD=90°,∠CDF+∠CAD=90°,
∴∠HGE=∠HEG.
∴EH=GH.
(3)解:如下图3所示,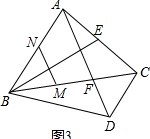
∵MN∥AD,∠BFA=∠CFD,
∴∠BMN=∠BFA.
∴∠BMN=∠CFD.
∵AB∥CD,
∴∠NBM=∠FCD.
在△BMN和△CFD中
$\left\{\begin{array}{l}{∠BMN=∠CFD}\\{BM=CF}\\{∠NBM=∠FCD}\end{array}\right.$
∴△BMN≌△CFD(ASA).
∴BN=CD.
又∵AE=CD=2,
∴BN=2.
点评 本题考查全等三角形的性质和判定、等腰直角三角形的性质,解题的关键是能根据题目中的条件推导出结论成立所需要的条件.

| A. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ |
| A. | 都是非负数 | B. | 都是负数 | C. | 都是正数 | D. | 其中有一个为0 |
 下面几何体的俯视图是( )
下面几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图几何体由棱长为2厘米的正方体组成.
如图几何体由棱长为2厘米的正方体组成.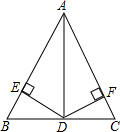 如图所示,已知在△ABC中,AD是∠BAC的平分线,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:BE=FC.
如图所示,已知在△ABC中,AD是∠BAC的平分线,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:BE=FC.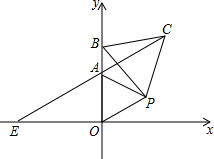 如图,在平面直角坐标系中,△AOP为等边三角形,A点坐标为(0,1),点B为y轴上位于A点上方的一个动点,以BP为边向BP的右侧作等边△PBC,连接CA,并延长CA交x轴于点E.
如图,在平面直角坐标系中,△AOP为等边三角形,A点坐标为(0,1),点B为y轴上位于A点上方的一个动点,以BP为边向BP的右侧作等边△PBC,连接CA,并延长CA交x轴于点E.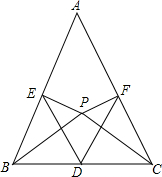 在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.
在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.