题目内容
2.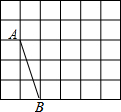 在如图所示的5×6方格中(每个方格的边长为1),点A、B在格点上.
在如图所示的5×6方格中(每个方格的边长为1),点A、B在格点上.(1)画等腰三角形ABC,使点C在格点上,且腰长为无理数.
(2)符合(1)中要求的等腰三角形可以画几个?
分析 (1)由勾股定理得出$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,即可画出等腰三角形;
(2)由(1)即可得出结果.
解答 解:(1)$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,如图所示:
(2)由(1)得:
符合(1)中要求的等腰三角形可以画5个.
点评 本题考查了勾股定理、正方形的性质、等腰三角形的判定;熟练掌握勾股定理,并能进行计算与作图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.方程组的$\left\{\begin{array}{l}{x+y=6}\\{x-y=4}\end{array}\right.$解为( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ |
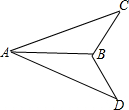 如图,已知AB平分∠CAD,AC=AD.求证:∠C=∠D.
如图,已知AB平分∠CAD,AC=AD.求证:∠C=∠D.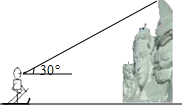 长春瓦萨国际滑雪节制作了很多雪雕,一名滑雪运动员的眼部距地面1.8米,他站在一座雪雕前观测这座雪雕顶部的仰角为30°,此时他的眼部到雪雕顶部的距离为4米,如图,那么雪雕的高度为6米.
长春瓦萨国际滑雪节制作了很多雪雕,一名滑雪运动员的眼部距地面1.8米,他站在一座雪雕前观测这座雪雕顶部的仰角为30°,此时他的眼部到雪雕顶部的距离为4米,如图,那么雪雕的高度为6米.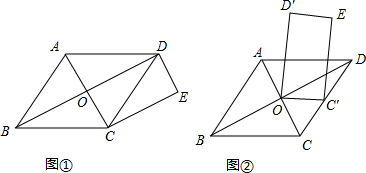
 如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=$\frac{k}{x}$的一支在第一象限交梯形对角线OC于点D,交边BC于点E.若点C的坐标为(2,2),则阴影部分面积S最小值为$\frac{3}{2}$.
如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=$\frac{k}{x}$的一支在第一象限交梯形对角线OC于点D,交边BC于点E.若点C的坐标为(2,2),则阴影部分面积S最小值为$\frac{3}{2}$. 如图几何体由棱长为2厘米的正方体组成.
如图几何体由棱长为2厘米的正方体组成.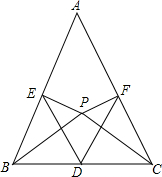 在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.
在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.