题目内容
2.计算与化简(1)化简(1+$\frac{2}{x-1}$)$÷\frac{x+1}{{x}^{2}-2x+1}$.
(2)解方程:$\frac{x}{x+1}-\frac{4}{{x}^{2}-1}=1$.
分析 (1)根据有括号先算括号内的,分式的除法法则进行计算即可;
(2)根据解分式方程的方法进行计算即可.
解答 解:(1)(1+$\frac{2}{x-1}$)$÷\frac{x+1}{{x}^{2}-2x+1}$
=$(\frac{x-1}{x-1}+\frac{2}{x-1})$×$\frac{(x-1)^{2}}{x+1}$
=$\frac{x+1}{x-1}×\frac{(x-1)^{2}}{x+1}$
=x-1;
(2)$\frac{x}{x+1}-\frac{4}{{x}^{2}-1}=1$
方程两边都乘以(x+1)(x-1),得
x(x-1)-4=(x+1)(x-1)
化简,得
x+3=0
解得,x=-3
检验:x=-3时,(x+1)(x-1)≠0.
故原分式方程的根是x=-3.
点评 本题考查分式的混合运算和解分式方程,解题的关键是注意解分式方程要检验.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
13.一元二次方程(m+1)x2+3x+m2-3m-4=0的一个根是0,则m的值为( )
| A. | 4或-1 | B. | 4 | C. | -1 | D. | -4或-1 |
10. 下面几何体的俯视图是( )
下面几何体的俯视图是( )
 下面几何体的俯视图是( )
下面几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
7.为了完成下列任务,你认为采用普查方式较为合适的是( )
| A. | 了解一批苹果是否甜 | |
| B. | 检测某种导弹的发射半径 | |
| C. | 调查深圳学生的“垃圾减量分类”的意识 | |
| D. | 检查“嫦娥5号”的所有零件是否合格 |
11.16的平方根是( )
| A. | ±4 | B. | 4 | C. | ±2 | D. | 2 |
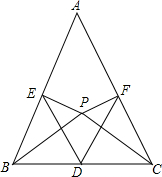 在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.
在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.