题目内容
7. A,B,C在一条直线上,△ABE与△BCD为等边三角形,AD与CE交于H,
A,B,C在一条直线上,△ABE与△BCD为等边三角形,AD与CE交于H,(1)说明∠AHE=60°.
(2)说明△BFG为等边三角形(或FG∥AC).
分析 (1)首先根据ASA证明△ABD≌△EBC,证明∠BAD=∠BEC,利用三角形的外角的性质即可证得;
(2)首先证明△ABF≌△EBG,证明BF=BG,即可证得△BFG是等边三角形,进而证明FG∥AC.
解答 解:(1)∵△ABE与△BCD为等边三角形,
∴∠ABE=∠CBD=60°,AB=BE,BC=BD,
∴∠ABD=∠EBC,
在△ABD和△EBC中,$\left\{\begin{array}{l}{AB=EB}\\{∠ABD=∠EBC}\\{BD=BC}\end{array}\right.$,
∴△ABD≌△EBC,
∴∠BAD=∠BEC,
∴∠AHE=∠BAD+∠ACE=∠BEC+∠ACE=∠ABE=60°;
(2)∵△ABD≌△EBC.
∴∠CAF=∠CEB,
又∵△ABC和△BCD都是等边三角形,且点A、B、C在同一条直线上,
∴∠EBD=180°-∠ABE-∠DBC=60°=∠ABE,
在△ABF和△EBG中,$\left\{\begin{array}{l}{∠ACD=∠BEG}\\{AB=BE}\\{∠ABF=EBG}\end{array}\right.$,
∴△ABF≌△EBG(ASA),
∴BF=BG,
又∵∠FBG=60°,
∴△BFG为等边三角形
∴∠FGB=∠GBC=60°,
∴FG∥AC.
点评 本题考查的是等边三角形的判定与性质及全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.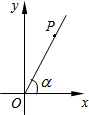 如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为α,则sinα的值为( )
如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为α,则sinα的值为( )
 如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为α,则sinα的值为( )
如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,4),且OP与x轴正半轴的夹角为α,则sinα的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
19.用平面去截一个几何体,如果截面的形状是圆,则原来的几何体的形状是( )
| A. | 圆柱 | B. | 圆锥 | C. | 球 | D. | 以上都有可能 |
16.现有3根木棒,其中两根的长度分别为4cm和6cm,若要用此3根木棒摆成一个三角形,则第三根的长度为( )
| A. | 2cm | B. | 4cm | C. | 10cm | D. | 12cm |
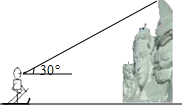 长春瓦萨国际滑雪节制作了很多雪雕,一名滑雪运动员的眼部距地面1.8米,他站在一座雪雕前观测这座雪雕顶部的仰角为30°,此时他的眼部到雪雕顶部的距离为4米,如图,那么雪雕的高度为6米.
长春瓦萨国际滑雪节制作了很多雪雕,一名滑雪运动员的眼部距地面1.8米,他站在一座雪雕前观测这座雪雕顶部的仰角为30°,此时他的眼部到雪雕顶部的距离为4米,如图,那么雪雕的高度为6米.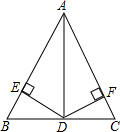 如图所示,已知在△ABC中,AD是∠BAC的平分线,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:BE=FC.
如图所示,已知在△ABC中,AD是∠BAC的平分线,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:BE=FC.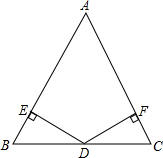 如图,D是△ABC的边BC上的中点,DE⊥AC于点E,DF⊥AB于点F,且BF=CE,求证:∠B=∠C.
如图,D是△ABC的边BC上的中点,DE⊥AC于点E,DF⊥AB于点F,且BF=CE,求证:∠B=∠C.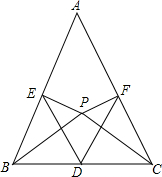 在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.
在△ABC中,AB=AC,D为BC边的中点,在三角形内部取一点P,使得∠ABP=∠ACP.过点P作PE⊥AC于点E,PF⊥AB于点F.