题目内容
11.计算(1)${(\frac{1}{2})^2}×\sqrt{{{(-2)}^2}}+\frac{1}{2}×\root{3}{-125}-{(-2)^3}×\root{3}{0.064}$
(2)$6\sqrt{2}+8\sqrt{2}-5\sqrt{2}$.
分析 (1)原式利用平方根、立方根定义,以及乘方的意义计算即可得到结果;
(2)原式合并同类二次根式即可得到结果.
解答 解:(1)原式=$\frac{1}{4}$×2+$\frac{1}{2}$×(-5)-(-8)×0.4=$\frac{1}{2}$-$\frac{5}{2}$+3.2=1.2;
(2)原式=(6+8-5)$\sqrt{2}$=9$\sqrt{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.已知一个等腰三角形的一条边长为6,另一条边长为13,则它的周长为( )
| A. | 25 | B. | 32 | C. | 25或32 | D. | 19 |
6. 如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=2,则AB的长是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=2,则AB的长是( )
 如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=2,则AB的长是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=2,则AB的长是( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 4$\sqrt{3}$ | D. | 6 |
20.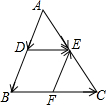 如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )
如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )
 如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )
如图,已知在△ABC中,点D、E、F分别是AB、AC、BC的中点.下列结论不正确的是( )| A. | $\overrightarrow{DE}$∥$\overrightarrow{BC}$ | B. | $\overrightarrow{AD}-\overrightarrow{AE}=\overrightarrow{DE}$ | C. | $\overrightarrow{DB}$=$-\overrightarrow{FE}$ | D. | $\overrightarrow{DB}+\overrightarrow{DE}+\overrightarrow{FE}=\overrightarrow{DE}$ |
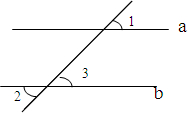 填空:如图,已知∠1=∠2,求证:a∥b
填空:如图,已知∠1=∠2,求证:a∥b 已知函数y=kx+b的图象与x轴、y轴分别交于点A(12,0)、点B,与函数y=x的图象交于点E,点E的横坐标为3,求:
已知函数y=kx+b的图象与x轴、y轴分别交于点A(12,0)、点B,与函数y=x的图象交于点E,点E的横坐标为3,求: 如图,点M,N分别在∠AOB的边OA,OB上,且OM=ON.
如图,点M,N分别在∠AOB的边OA,OB上,且OM=ON.