题目内容
3.将抛物线y=x2-1向左平移2个单位得到抛物线C1,抛物线C1与x轴交于A,B两点,与y轴交于C点,其顶点为M.(1)求A,B,M点的坐标;
(2)将图1中△AOC沿x轴向左平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△AMC重叠的面积记为s,用m的代数式表示s.
(3)如图2,设S(-2,0),过点S任作直线EF交抛物线C1于E,F两点,点P为EF的中点,求证:PF=PM.
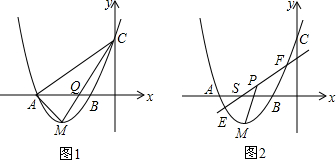
分析 (1)根据平移的方法左加右减,写出抛物线的解析式即可解决问题.
(2)①当0<m≤$\frac{3}{2}$时,根据s=S△AFC-S△NEC进行计算,②如图2中,当$\frac{3}{2}$<m<3时,根据s=${S}_{△A{O}_{1}N}$进行计算.
(3)利用方程组求出线段EF、点P坐标,根据两点距离公式求出PM,比较结果即可解决问题.
解答 解:(1)由题意抛物线C1为y=(x+2)2-1=x2+4x+3,
令y=0得x2+4x+3=0,解得x=-1或-3,
∴点A(-1,0),点B(-3,0),顶点M坐标(-2,-1).
(2)如图1中,当0<m≤$\frac{3}{2}$时,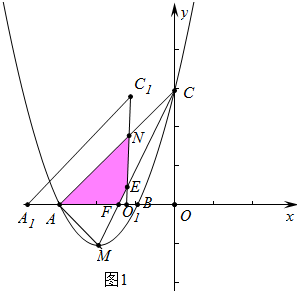
∵直线AC为y=x+3,直线MC为y=2x+3,点O1(-m,0),
∴点N(-m,-m+3),点E(-m,-2m+3),点F(-$\frac{3}{2}$,0),
∴s=S△AFC-S△NEC=$\frac{1}{2}$×$\frac{3}{2}$×3-$\frac{1}{2}$(-m+3+2m-3)•m=-$\frac{1}{2}$m2+$\frac{9}{4}$.
如图2中,当$\frac{3}{2}$<m<3时,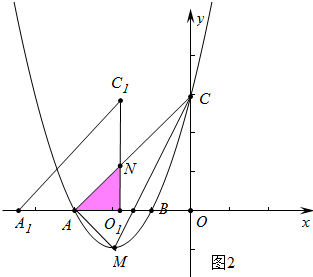
∵AO=OC,∠AOC=90°,
∴∠CAO=∠ACO=45°,
∵∠AO1N=90°,
∴∠O1AN=∠O1NA=45°,
∴AO1=O1N=3-m,
∴s=${S}_{△A{O}_{1}N}$=$\frac{1}{2}$(3-m)2.
综上所述s=$\left\{\begin{array}{l}{-\frac{1}{2}{m}^{2}+\frac{9}{4}}&{(0<m≤\frac{3}{2})}\\{\frac{1}{2}(3-m)^{2}}&{(\frac{3}{2}<m<3)}\end{array}\right.$.
(3)如图3中,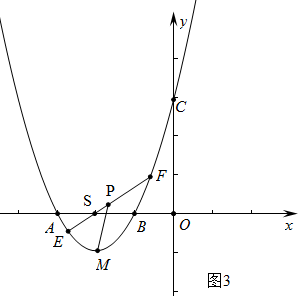
设点E(x1,y1),F(x2,y2),直线EF为y=kx+b,把点S(-2,0)代入得到,b=2K,
∴直线EF为y=kx+2k.
由$\left\{\begin{array}{l}{y=kx+2k}\\{y={x}^{2}+4x+3}\end{array}\right.$消去y得x2+(4-k)x+3-2k=0,
∴x1+x2=k-4,x1x2=3-2k,y1+y2=k2,y1y2=(kx1+2k)(kx2+2k)=k2x1x2+2k2(x1+x2)+4k2=-k2,
∴点P坐标($\frac{k-4}{2}$,$\frac{{k}^{2}}{2}$),∵点M(-2,-1),
∴PM=$\sqrt{(\frac{k-4}{2}+2)^{2}+(\frac{{k}^{2}}{2}+1)^{2}}$=$\frac{1}{2}$$\sqrt{{k}^{4}+5{k}^{2}+4}$.
EF=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}+({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{(k-4)^{2}-4(3-2k)+{k}^{4}+4{k}^{2}}$=$\sqrt{{k}^{4}+5{k}^{2}+4}$,
∴PM=$\frac{1}{2}$EF=PF.
点评 本题考查二次函数、一次函数、平移、三角形面积,根与系数的关系等知识,正确画出图形是解决问题的关键,掌握抛物线平移的规律:左加右减,上加下减,有一定的代数化简技巧,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案 如图,一艘轮船在B处观测灯塔A位于南偏东50°方向上,相距40海里,轮船从B处沿南偏东20°方向匀速航行至C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
如图,一艘轮船在B处观测灯塔A位于南偏东50°方向上,相距40海里,轮船从B处沿南偏东20°方向匀速航行至C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )| A. | 20海里 | B. | 40海里 | C. | 20$\sqrt{3}$海里 | D. | 40$\sqrt{3}$海里 |
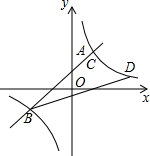 如图,一次函数y=kx+1(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,其中点A的坐标为(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点C,D.
如图,一次函数y=kx+1(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,其中点A的坐标为(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点C,D.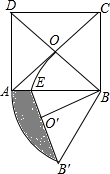 如图,在正方形ABCD中,对角线AC、BD相交于点O,△AOB绕点B逆时针旋转60°得到△BO′B′,AB与弧OO′相交于点E,若AD=2,则图中阴影部分的面积是$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.
如图,在正方形ABCD中,对角线AC、BD相交于点O,△AOB绕点B逆时针旋转60°得到△BO′B′,AB与弧OO′相交于点E,若AD=2,则图中阴影部分的面积是$\frac{2π}{3}$-$\frac{\sqrt{6}}{2}$.