题目内容
12.分别求出下列事件的概率:(1)在52张不同的纸牌(除去大、小王后)中,随机抽出一张是“A”的概率;
(2)在1~10这10个数字中随机取出一个数,是3的倍数的概率;
(3)一个袋子中装有15个球,其中有10个红球,随机摸出一个球不是红球的概率.
分析 (1)只需知道52张不同的纸牌中有几张A,就可解决问题;
(2)只需知道在1~10这10个数字中3的倍数有几个,就可解决问题;
(3)只需知道15个球中有几个球不是红球,就可解决问题.
解答 解:(1)由于52张不同的纸牌中有4张A,
因此P(抽到A)=$\frac{4}{52}$=$\frac{1}{13}$;
(2)由于在1~10这10个数字中,是3的倍数的有3,6,9三个数,
因此P(取出的是3的倍数)=$\frac{3}{10}$;
(3)由于15个球中不是红球的有15-10=5(个),
因此P(摸出的不是红球)=$\frac{5}{15}$=$\frac{1}{3}$.
点评 本题主要考查的概率公式的运用,概率公式为P(A)=$\frac{m}{n}$,其中n表示某试验中共有n种等可能结果,其中事件A发生的可能性共有m种.

练习册系列答案
相关题目
1.过多边形的一个顶点的所有对角线,将这个多边形分成7个三角形,这个多边形的内角和等于( )
| A. | 900° | B. | 1260° | C. | 1440° | D. | 1800° |
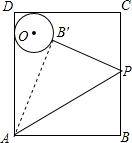 如图,矩形ABCD中,AB=20,AD=25,矩形内有一点O,以O为圆心,5为半径画圆,与AD,CD都相切,点P是BC上一点,将△ABP沿着AP对折得到△AB′P,若AB′与⊙O相切于点B′.则BP的长度是12.
如图,矩形ABCD中,AB=20,AD=25,矩形内有一点O,以O为圆心,5为半径画圆,与AD,CD都相切,点P是BC上一点,将△ABP沿着AP对折得到△AB′P,若AB′与⊙O相切于点B′.则BP的长度是12.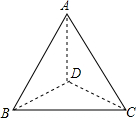 如图是正四面体(四个面都是正三角形的三棱锥)小木块(质地均匀)的一个顶点,将木块随机投掷在水平桌面上.则A与桌面接触的概率是$\frac{3}{4}$.
如图是正四面体(四个面都是正三角形的三棱锥)小木块(质地均匀)的一个顶点,将木块随机投掷在水平桌面上.则A与桌面接触的概率是$\frac{3}{4}$. 如图,AC,BD相交于点O,AB∥CD,AD∥BC,E,F分别是OB,OD的中点,求证:四边形AFCE是平行四边形.
如图,AC,BD相交于点O,AB∥CD,AD∥BC,E,F分别是OB,OD的中点,求证:四边形AFCE是平行四边形.