题目内容
1. 已知:如图,△ABC的外接圆是⊙O,AD是BC边上的高.
已知:如图,△ABC的外接圆是⊙O,AD是BC边上的高.(1)请用尺规作出⊙O(不写作法,保留作图痕迹);
(2)若AB=8,AC=6,AD=5.4,求⊙O的半径.
分析 (1)作三角形两边的垂直平分线,交点即为圆心O,以OA为半径画圆,⊙O即为所求;
(2)如图,作⊙O的直径AE,连接BE. 由△ABE∽△ADC,可得$\frac{AB}{AD}$=$\frac{AE}{AC}$,由此即可解决问题;
解答 解:(1)如图,⊙O是所求作的图形. 
(2)如图,作⊙O的直径AE,连接BE.
∵AE是直径,
∴∠ABE=90°.
∵∠ADC=∠ABE=90°,∠C=∠E,
∴△ABE∽△ADC,
∴$\frac{AB}{AD}$=$\frac{AE}{AC}$.即 $\frac{8}{5.4}$=$\frac{AE}{6}$,
解得AE=$\frac{80}{9}$.
∴⊙O的半径为$\frac{40}{9}$.
点评 本题考查复杂作图、三角形的外接圆与外心、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.已知,二次函数y=x2+bx-2017的图象与x轴交于点A(x1,0)、B(x2,0)两点,则当x=x1+x2时,则y的值为( )
| A. | 2019 | B. | 2017 | C. | 2018 | D. | -2017 |
 如图,在正方形ABCD内部放置了两个全等的Rt△ADE,Rt△BCF,已知正方形ABCD的边长为6,∠ADE=∠FBC=30°,那么线段EF的长为3($\sqrt{6}$-$\sqrt{2}$).
如图,在正方形ABCD内部放置了两个全等的Rt△ADE,Rt△BCF,已知正方形ABCD的边长为6,∠ADE=∠FBC=30°,那么线段EF的长为3($\sqrt{6}$-$\sqrt{2}$). 如图,直线y=kx+b与双曲线y=$\frac{m}{x}$的一支交于点A,点B,与x轴交于点C,已知点A的坐标是(1,6),AB=2BC.
如图,直线y=kx+b与双曲线y=$\frac{m}{x}$的一支交于点A,点B,与x轴交于点C,已知点A的坐标是(1,6),AB=2BC.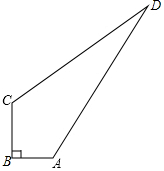 如图,有一块四边形空地ABCD,AB=3cm,BC=4cm,CD=12cm,DA=13cm,∠B=90°.现要在空地处种植草坪,求草坪的种植面积.
如图,有一块四边形空地ABCD,AB=3cm,BC=4cm,CD=12cm,DA=13cm,∠B=90°.现要在空地处种植草坪,求草坪的种植面积.