Question

10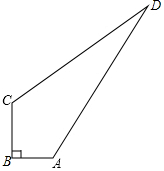．如图，有一块四边形空地ABCD，AB=3cm，BC=4cm，CD=12cm，DA=13cm，∠B=90°．现要在空地处种植草坪，求草坪的种植面积．

Answer 1

分析 首先连接AC，利用勾股定理计算出AC的长，再利用勾股定理逆定理判定△ACD为直角三角形，然后可求面积．

解答 解：连接AC，
∵AB=3，BC=4，∠B=90°，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5，
∵5²+12²=13²，
∴AC²+DC²=AD²，
∴△ACD为直角三角形，
∴S_{四边形ABCD的面积}=S_△ABC+S_△ACD=$\frac{1}{2}$AB•BC+$\frac{1}{2}$AC•CD=$\frac{1}{2}$×3×4+$\frac{1}{2}$×12×5=36．

点评 此题主要考查了勾股定理的运用，以及勾股定理逆定理，关键是掌握三角形两边的平方和等于第三边的平方时，此三角形是直角三角形．