题目内容
9. 如图,直线y=kx+b与双曲线y=$\frac{m}{x}$的一支交于点A,点B,与x轴交于点C,已知点A的坐标是(1,6),AB=2BC.
如图,直线y=kx+b与双曲线y=$\frac{m}{x}$的一支交于点A,点B,与x轴交于点C,已知点A的坐标是(1,6),AB=2BC.(1)求直线与双曲线的解析式.
(2)求△OAB的面积.
分析 (1)根据(1,6)可得双曲线的解析式,进而求得B(3,2),再根据待定系数法即可得到直线的解析式;
(2)先根据直线的解析式为y=-2x+8,求得OC=4,再根据S△OAB=S△OAC-S△OCB进行计算即可得到△OAB的面积.
解答 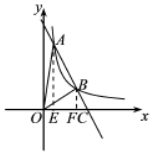 解:(1)把(1,6)代入双曲线y=$\frac{m}{x}$,可得m=1×6=6,
解:(1)把(1,6)代入双曲线y=$\frac{m}{x}$,可得m=1×6=6,
∴双曲线的解析式为y=$\frac{6}{x}$,
如图,作AE⊥x轴于E,AF⊥x轴于F,则AE∥BF,AE=6,
∵AB=2BC,AE∥BF,
∴$\frac{AE}{BF}$=$\frac{AC}{BC}$=3,即$\frac{6}{BF}$=3,
∴BF=2,
当y=2时,2=$\frac{6}{x}$,即x=3,
∴B(3,2),
把(1,6),(3,2)代入直线y=kx+b,可得
$\left\{\begin{array}{l}{k+b=6}\\{3k+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$,
∴直线的解析式为y=-2x+8.
(2)由0=-2x+8,可得x=4,
∴C(4,0),即OC=4,
∴S△OAB=S△OAC-S△OCB=$\frac{1}{2}$×4×6-$\frac{1}{2}$×4×2=8(平方单位).
点评 本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与一次函数交点坐标同时满足反比例函数与一次函数解析式.

练习册系列答案
相关题目
17. 为了治理大气污染,某城市抽取了该地区一年中某些天的空气质量指数,绘制了如下的统计图表:
为了治理大气污染,某城市抽取了该地区一年中某些天的空气质量指数,绘制了如下的统计图表:
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=6,m=50;
(2)“轻度污染”所对应扇形的圆心角是72度;
(3)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前统计,请你估计一年(365天)该市有多少天不适宜开展户外活动.(结果保留整数)
 为了治理大气污染,某城市抽取了该地区一年中某些天的空气质量指数,绘制了如下的统计图表:
为了治理大气污染,某城市抽取了该地区一年中某些天的空气质量指数,绘制了如下的统计图表:| 级别 | 指数 | 天数 |
| 1级:优 | 0-50 | 3 |
| 2级:良 | 51-100 | 24 |
| 3级:轻度污染 | 101-200 | 10 |
| 度污染 | 201-300 | 7 |
| 5级:重度污染 | 大于300 | a |
| 合计 | m |
(1)空气质量指数统计表中的a=6,m=50;
(2)“轻度污染”所对应扇形的圆心角是72度;
(3)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前统计,请你估计一年(365天)该市有多少天不适宜开展户外活动.(结果保留整数)
4.某“优质花海专用花籽”的价格为60元/kg,如果一次性购买5kg以上的花籽,超过5kg的部分的花籽的价格打8折.
(1)根据题意,填写下表:
(2)设购买花籽的重量为xkg,付款金额为y元,求y关于x的函数解析式;
(3)若花海园丁李伯伯一次购买该花籽花费了540元,求他购买花籽的重量.
(1)根据题意,填写下表:
| 购买花籽的重量/kg | 3 | 4 | 5 | 6 | … |
| 付款金额/元 | 180 | 240 | 300 | 348 |
(3)若花海园丁李伯伯一次购买该花籽花费了540元,求他购买花籽的重量.
14.由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表所示:
(1)若该公司五月份的销售收入为330万元,求甲、乙两种型号的产品分别生产多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过216万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入-投入总成本)
 | 甲 | 乙 |
| 原料成本 | 12 | 8 |
| 销售单价 | 18 | 12 |
| 生产提成 | 1 | 0.6 |
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过216万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入-投入总成本)
18.过12边形的每一个顶点有( )条对角线.
| A. | 9 | B. | 10 | C. | 8 | D. | 11 |
19.下列事件:①三角形的外角和是180°;②四边形的内角和是360°;③正五边形有6条对角线;其中属于确定事件的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |

 已知:如图,△ABC的外接圆是⊙O,AD是BC边上的高.
已知:如图,△ABC的外接圆是⊙O,AD是BC边上的高.