题目内容
11.下列关于x的方程中,一定有实数根的是( )| A. | $\sqrt{x-1}+4=0$ | B. | x2+x+1=0 | C. | $\sqrt{x}=-x$ | D. | $\sqrt{x-2}+\sqrt{2-x}=-1$ |
分析 根据$\sqrt{a}$表示a的算术平方根,一定是非负数,以及一元二次方程根的判别式即可作出判断.
解答 解:A、$\sqrt{x-1}$≥0,4>0,则原式一定不成立,则方程没有实数根,选项错误;
B、a=1,b=1,c=1,则△=b2-4ac=1-4=-3<0,则方程无实数根,选项错误;
C、当x=0时,$\sqrt{x}$=-x一定成立,即方程有实数根0,选项正确;
D、$\sqrt{x-2}$≥0,$\sqrt{2-x}$≥0,则$\sqrt{x-2}$+$\sqrt{2-x}$=0,因而$\sqrt{x-2}$+$\sqrt{2-x}$=-1一定不成立,没有实数根,选项错误.
故选C.
点评 本题考查了算术平方根的定义以及一元二次方程根的判别式,理解任何非负数的算术平方根是非负数是关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
6.关于立方根,下列说法正确的是( )
| A. | 正数有两个立方根 | B. | 立方根等于它本身的数只有0 | ||
| C. | 负数的立方根是负数 | D. | 负数没有立方根 |
20. 如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )
如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )
 如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )
如图,△ABC中,∠A=52°,O是边AB和边AC的垂直平分线的交点,那么∠OCB=( )| A. | 36° | B. | 120° | C. | 38° | D. | 76° |
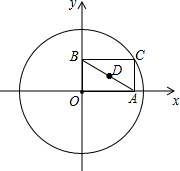 如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是B的中点,如果点C在圆上运动一周,那么点D运动过的路程长为2π.
如图,⊙O的半径为2,点C是圆上的一个动点,CA⊥x轴,CB⊥y轴,垂足分别为A、B,D是B的中点,如果点C在圆上运动一周,那么点D运动过的路程长为2π.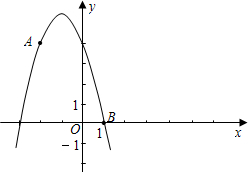 如图,已知A(-2,4)和B(1,0)都在抛物线$y=-\frac{4}{3}{x^2}-\frac{8}{3}x+4$
如图,已知A(-2,4)和B(1,0)都在抛物线$y=-\frac{4}{3}{x^2}-\frac{8}{3}x+4$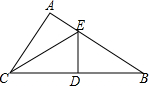 如图,在Rt△ABC中,∠A=90°,边BC的垂直平分线DE交AB于点E,连接CE.求证:BE2=AC2+AE2.
如图,在Rt△ABC中,∠A=90°,边BC的垂直平分线DE交AB于点E,连接CE.求证:BE2=AC2+AE2.