题目内容
20．
如图，△ABC中，∠A=52°，O是边AB和边AC的垂直平分线的交点，那么∠OCB=（ ）| A． | 36° | B． | 120° | C． | 38° | D． | 76° |
分析 连接OB，根据题意得到点O是△ABC的外心，根据圆周角定理求出∠BOC的度数，根据等腰三角形的性质计算即可．
解答 解：
连接OB，
∵O是边AB和边AC的垂直平分线的交点，
∴点O是△ABC的外心，OB=OC，
∴∠BOC=2∠A=104°，
∴∠OCB=∠OBC=$\frac{1}{2}$（180°-104°）=38°，
故选：C．
点评 本题考查的是线段垂直平分线的性质和圆周角定理的应用，掌握三角形三边垂直平分线的交点是三角形的外心、外心到三个顶点的距离相等是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．下列关于x的方程中，一定有实数根的是（ ）
| A． | $\sqrt{x-1}+4=0$ | B． | x2+x+1=0 | C． | $\sqrt{x}=-x$ | D． | $\sqrt{x-2}+\sqrt{2-x}=-1$ |
8．若等边△ABC的边长为4cm，那么△ABC的面积为（ ）
| A． | 2$\sqrt{3}$cm2 | B． | 4$\sqrt{3}$cm2 | C． | 6$\sqrt{3}$cm2 | D． | 8cm2 |
15．
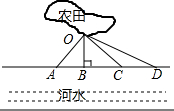春节过后，某村计划挖一条水渠将不远处的河水引到农田（记作点O），以便对农田的小麦进行灌溉，现设计了四条路段OA，OB，OC，OD，如图所示，其中最短的一条路线是（ ）
春节过后，某村计划挖一条水渠将不远处的河水引到农田（记作点O），以便对农田的小麦进行灌溉，现设计了四条路段OA，OB，OC，OD，如图所示，其中最短的一条路线是（ ）| A． | OA | B． | OB | C． | OC | D． | OD |
如图，将三角形ABC沿着DE折叠，使点A落在BC上的点F处，且DE∥BC，若∠B=70°，则∠BDF=40°．