题目内容

1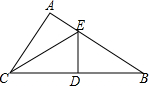．如图，在Rt△ABC中，∠A=90°，边BC的垂直平分线DE交AB于点E，连接CE．求证：BE2=AC2+AE2．

分析 根据线段垂直平分线的性质可得EB=EC，再根据条件CE2=AC2+AE2可得BE2=AC2+AE2．

解答 证明：∵如图，边BC的垂直平分线DE交AB于点E，
∴CE=BE．
∵在Rt△ABC中，∠A=90°，
∴由勾股定理得到：CE2=AC2+AE2
∴BE2=AC2+AE2．

点评 此题主要考查了勾股定理，线段垂直平分线的性质：垂直平分线上任意一点，到线段两端点的距离相等．

练习册系列答案
相关题目
11．下列关于x的方程中，一定有实数根的是（　　）
A．$\sqrt{x-1}+4=0$B．x2+x+1=0C．$\sqrt{x}=-x$D．$\sqrt{x-2}+\sqrt{2-x}=-1$
12．如图，将三角形ABC沿着DE折叠，使点A落在BC上的点F处，且DE∥BC，若∠B=70°，则∠BDF=40°．
9．2m=a，2n=b，则22m+3n=a2b3（用a、b的代数式表示）．
16．计算：
（1）（$\sqrt{24}-\sqrt{2}$）-（$\sqrt{8}+\sqrt{6}$）
（2）2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$$÷\sqrt{2}$
（3）（2$\sqrt{48}$-3$\sqrt{27}$）$÷\sqrt{6}$
（4）（7+4$\sqrt{3}$）（2-$\sqrt{3}$）2+（2+$\sqrt{3}$）（2-$\sqrt{3}$）+$\sqrt{3}$．
6．若关于x、y的方程组$\left\{\begin{array}{l}2x+y=k\\ x+2y=3\end{array}\right.$的解也是方程x+y=1的解，求k的值．
13．若4a2-2ka+9是一个完全平方的展开形式，则k的值为（　　）
A．6B．±6C．12D．±12
10．计算：
（1）2$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{1}{3}}$+$\sqrt{8}$
（2）2$\sqrt{10}$×$3\sqrt{5}$-4$\sqrt{2}$
（3）（3$\sqrt{48}$-2$\sqrt{27}$）$÷\sqrt{3}$
（4）$\sqrt{1\frac{2}{3}}÷\sqrt{2\frac{1}{3}}×\sqrt{1\frac{2}{5}}$．
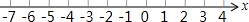11．解不等式组：$\left\{\begin{array}{l}{2x＞3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$，并把解集在数轴上表示出来．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网