题目内容
1.计算:$\frac{\frac{1}{2}}{1+\frac{1}{2}}$+$\frac{\frac{1}{3}}{(1+\frac{1}{2})(1+\frac{1}{3})}$+$\frac{\frac{1}{4}}{(1+\frac{1}{2})(1+\frac{1}{3})(1+\frac{1}{4})}$+…+$\frac{\frac{1}{2010}}{(1+\frac{1}{2})(1+\frac{1}{3})…(1+\frac{1}{2010})}$.分析 先计算分母小括号里面的加法,再约分计算分母,再约分计算各分数得到原式=$\frac{2}{2×3}$+$\frac{2}{3×4}$+$\frac{2}{4×5}$+…+$\frac{2}{2010×2011}$,再拆分抵消即可求解.
解答 解:$\frac{\frac{1}{2}}{1+\frac{1}{2}}$+$\frac{\frac{1}{3}}{(1+\frac{1}{2})(1+\frac{1}{3})}$+$\frac{\frac{1}{4}}{(1+\frac{1}{2})(1+\frac{1}{3})(1+\frac{1}{4})}$+…++…+$\frac{\frac{1}{2010}}{(1+\frac{1}{2})(1+\frac{1}{3})…(1+\frac{1}{2010})}$
=$\frac{\frac{1}{2}}{\frac{3}{2}}$+$\frac{\frac{1}{3}}{\frac{3}{2}×\frac{4}{3}}$+$\frac{\frac{1}{4}}{\frac{3}{2}×\frac{4}{3}×\frac{5}{4}}$+…+$\frac{\frac{1}{2010}}{\frac{3}{2}×\frac{4}{3}×…×\frac{2011}{2010}}$
=$\frac{2}{2×3}$+$\frac{2}{3×4}$+$\frac{2}{4×5}$+…+$\frac{2}{2010×2011}$
=2×($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{2010}$-$\frac{1}{2011}$)
=2×($\frac{1}{2}$-$\frac{1}{2011}$)
=2×$\frac{2009}{4022}$
=$\frac{2009}{2011}$.
点评 考查了有理数的混合运算,本题难度和计算量较大,关键是变形得到原式=$\frac{2}{2×3}$+$\frac{2}{3×4}$+$\frac{2}{4×5}$+…+$\frac{2}{2010×2011}$.

 阅读快车系列答案
阅读快车系列答案 请只用无刻度的直尺作图:在图中的正方形网格边长均为1,在图(1)中作一个面积为12的菱形;在图(2)中作一个面积为13的正方形.
请只用无刻度的直尺作图:在图中的正方形网格边长均为1,在图(1)中作一个面积为12的菱形;在图(2)中作一个面积为13的正方形.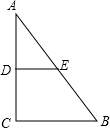 如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.
如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.