题目内容
16.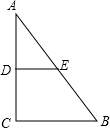 如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.
如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.
分析 由DE∥BC,知△ADE∽△ACB,根据相似三角形的面积比等于相似比的平方,即可解决问题.
解答 解:∵∠C=90°,AB=5,BC=3.
∴AC=4,
∵DE∥BC,
∴△ADE∽△ACB,
∴$\frac{S△ADE}{S△ACB}=(\frac{AD}{AC})^{2}=(\frac{4-x}{4})^{2}$,
∵S△ABC=6,
∴S△ADE=6×($\frac{4-x}{4}$)2,
∴y=S△ABC-S△ADE=6-6×($\frac{4-x}{4}$)2=-$\frac{3}{8}$x2+3x(0<x<4).
点评 本题主要考查了相似三角形的判定与性质以及列函数表达式,熟悉相似三角形的判定和性质是解决问题的关键.

练习册系列答案
相关题目
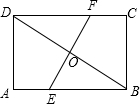 如图所示,在矩形ABCD中,EF是BD的垂直平分线,BD=40米,EF=30米,求证四边形BEDF是菱形,并求出它的面积.
如图所示,在矩形ABCD中,EF是BD的垂直平分线,BD=40米,EF=30米,求证四边形BEDF是菱形,并求出它的面积.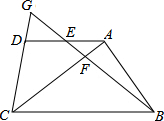 如图,在梯形ABCD中,AD∥BC,点E是边AD的中点,连接BE,交AC于点F,BE的延长线交CD的延长线于点G.
如图,在梯形ABCD中,AD∥BC,点E是边AD的中点,连接BE,交AC于点F,BE的延长线交CD的延长线于点G.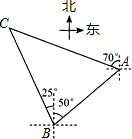 如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)
如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)