题目内容
6.计算题:$\sqrt{45}$+$\frac{4}{\sqrt{2}}$+$\sqrt{18}$-$\sqrt{80}$+$\sqrt{(\sqrt{2}-\sqrt{5})^{2}}$.分析 先进行二次根式的化简,然后合并.
解答 解:原式=3$\sqrt{5}$+2$\sqrt{2}$+3$\sqrt{2}$-4$\sqrt{5}$+$\sqrt{5}$-$\sqrt{2}$
=4$\sqrt{2}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简以及合并.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
16.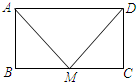 如图,已知点M为矩形ABCD中边BC的中点,若要使△AMD为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是( )
如图,已知点M为矩形ABCD中边BC的中点,若要使△AMD为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是( )
 如图,已知点M为矩形ABCD中边BC的中点,若要使△AMD为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是( )
如图,已知点M为矩形ABCD中边BC的中点,若要使△AMD为等腰直角三角形,则再须添加一条件;那么在下列给出的条件中,错误的是( )| A. | ∠AMD=90° | B. | AM是∠BAD的平分线 | ||
| C. | AM:AD=1:$\sqrt{2}$ | D. | AB:BC=1:$\sqrt{2}$ |
18.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调研发现:该品牌玩具每天的销售量y件与售价x元之间存在着如下表所示的一次函数关系.
(1)求销售量y(件)与售价x(元)之间的函数关系式;
(2)设销售该品牌玩具获得的利润为W元,求出W与x之间的函数关系式;当商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
| 售价x(元) | … | 70 | 90 | … |
| 销售量y(件) | … | 300 | 100 | … |
(2)设销售该品牌玩具获得的利润为W元,求出W与x之间的函数关系式;当商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
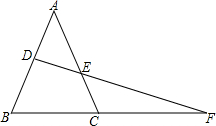 如图,在△ABC中,D为AB的中点,DF交AC于E,交BC的延长线于F,求证:AE•CF=BF•EC.
如图,在△ABC中,D为AB的中点,DF交AC于E,交BC的延长线于F,求证:AE•CF=BF•EC.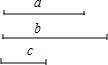 已知:线段a、b、c,如图所示,求作:线段x,使2a:b=3c:x.
已知:线段a、b、c,如图所示,求作:线段x,使2a:b=3c:x.