题目内容
11.已知$\sqrt{{(x+3)}^{2}{+y}^{2}}$+$\sqrt{{(x-3)}^{2}{+y}^{2}}$=10,求$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$.分析 把带根号的一项移项后平方,整理后再平方,然后整理即可得解.
解答 解:移项得,$\sqrt{{(x+3)}^{2}{+y}^{2}}$=10-$\sqrt{{(x-3)}^{2}{+y}^{2}}$,
两边平方得,(x+3)2+y2=100-20$\sqrt{{(x-3)}^{2}{+y}^{2}}$+(x-3)2+y2,
整理得,5$\sqrt{{(x-3)}^{2}{+y}^{2}}$=25-3x,
两边平方得,25x2-150x+225+25y2=625-150x+9x2,
所以,16x2+25y2=400,
两边除以400得,$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1.
点评 本题考查了非负数的性质,此类题目,难点在于把两个算术平方根通过移项分到等式左右两边.

练习册系列答案
相关题目
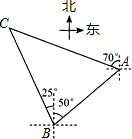 如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)
如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)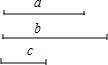 已知:线段a、b、c,如图所示,求作:线段x,使2a:b=3c:x.
已知:线段a、b、c,如图所示,求作:线段x,使2a:b=3c:x.