题目内容
7.$\sqrt{{x}^{2}+2x+2}$+$\sqrt{(x-2)^{2}+16}$的最小值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{34}$ | C. | $\sqrt{17}$ | D. | 均不是 |
分析 根据题意结合两点之间距离求法,利用轴对称求出最短路线进而得出答案.
解答  解:原式=$\sqrt{(x+1)^{2}+1}$+$\sqrt{(x-2)^{2}+16}$,
解:原式=$\sqrt{(x+1)^{2}+1}$+$\sqrt{(x-2)^{2}+16}$,
即x轴上的点到(-1,1)和(2,4)的距离之和的最小值
画图可知,
点(4,2)关于x轴的对称点(4,-2)与(-1,1)连线与x轴的交点即为所求,
此时最小值为:$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$.
故选:B.
点评 此题主要考查了无理函数的最值,利用数形结合得出函数最值是解题关键.

练习册系列答案
相关题目
 如图,数轴上有A,B两点,点A运动的速度是每秒2个单位,点B运动的速度是每秒1个单位.
如图,数轴上有A,B两点,点A运动的速度是每秒2个单位,点B运动的速度是每秒1个单位.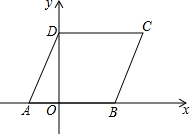 如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.
如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.