题目内容
18.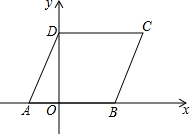 如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.
如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.
分析 在△AOD中可求得OD、AD,根据菱形的性质可知CD=AD=AB,可求得C点坐标,再根据菱形的面积公式可求得其面积.
解答 解:∵A(-3,0),
∴OA=3,
∵∠DAB=60°,
∴AD=2AO=6,OD=$\sqrt{3}$OA=3$\sqrt{3}$,
∵四边形ABCD为菱形,
∴AB=CD=AD=6,
∴C点坐标为(6,3$\sqrt{3}$),
∴S菱形ABCD=AB•OD=6×3$\sqrt{3}$=18$\sqrt{3}$.
点评 本题主要考查菱形的性质,掌握菱形是四边相等的平行四边形是解题的关键,注意菱形两个面积公式的灵活运用.

练习册系列答案
相关题目
7.$\sqrt{{x}^{2}+2x+2}$+$\sqrt{(x-2)^{2}+16}$的最小值为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{34}$ | C. | $\sqrt{17}$ | D. | 均不是 |
13.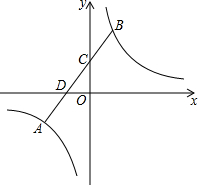 如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
 如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )| A. | AD>BC | B. | AD=BC | C. | AD<BC | D. | 无法判断 |
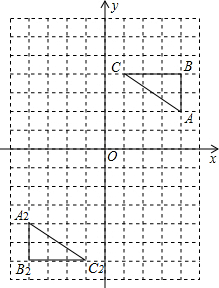 如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,点A的坐标(4,2)
如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,点A的坐标(4,2)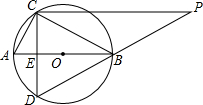 如图,AB为⊙O直径,C为圆上一点,AC=2,BC=4,E为直径AB上一动点(不与点A、B重合),CE延长线交⊙O于D,PC⊥CD交DB延长线于点P.
如图,AB为⊙O直径,C为圆上一点,AC=2,BC=4,E为直径AB上一动点(不与点A、B重合),CE延长线交⊙O于D,PC⊥CD交DB延长线于点P.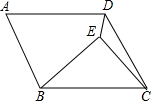 如图,在?ABCD内有一点E,如果满足∠EDA=90°,∠EBC=∠EDC,∠ECB=45°,试问是否有与BE相等的线段?
如图,在?ABCD内有一点E,如果满足∠EDA=90°,∠EBC=∠EDC,∠ECB=45°,试问是否有与BE相等的线段?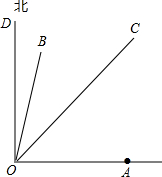 如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A.
如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A.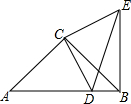 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2$\sqrt{2}$.点D在边AB上,不与点A,B重合,连接CD,过点C作CE⊥CD,且CE=CD,连接DE、BE.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2$\sqrt{2}$.点D在边AB上,不与点A,B重合,连接CD,过点C作CE⊥CD,且CE=CD,连接DE、BE.