题目内容
19.甲、乙两商店以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲店累计购买100元商品后,再购买的商品按原价的90%收费;在乙店累计购买50元商品后,在购买的商品按原价的95%收费,顾客怎样选择商店购物才能获得更大优惠?这个问题比较复杂,从何处入手考虑呢?
甲商店的优惠方案的起点为购物款达100元;
乙商店的优惠方案的起点为购物款达50元.
我们是否应分情况考虑?可以怎样分情况呢?
如果累计购物不超过50元,则在两店购物花费有区别吗?
分析 设购物x元,分别计算出①x≤50元,②50<x<100元,③x≥100元时辆家店得到的实惠,然后可作出判断.
解答 解:甲商店的优惠方案的起点为购物款达100元;
乙商店的优惠方案的起点为购物款达50元.
①当x≤50元,此时甲乙两店都不能享受到优惠,故选两家中的任意一家都行;
②当50<x<100元,此时在甲店享受不到优惠,而在乙店可以享受到(x-50)×5%的优惠;
③当x≥100元,此时在甲店享受的优惠为(x-100)×10%,在乙店享受到得优惠为(x-50)×5%,
若(x-100)×10%=(x-50)×5%,
解得:x=150,
综上可得:如果购物在50元以内去两家都可以,如果购物在50至100之间则去乙店,如果购物在100至150之间去乙店实惠,如果购物等于150去两家任意一家都可以,如果购物超过250去甲店合适.
点评 本题考查了一元一次方程的应用,两家的优惠政策不一样,要分类进行讨论,得出不同的购物钱数的不同选择.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.$\sqrt{{x}^{2}+2x+2}$+$\sqrt{(x-2)^{2}+16}$的最小值为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{34}$ | C. | $\sqrt{17}$ | D. | 均不是 |
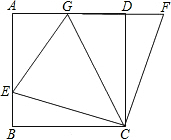 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,G在AD上,且DF=BE.①CE=CF;②EC⊥CF;③△ECG≌△FCG,④若∠GCE=45°,则EG=BE+GD,以上说法正确的是①②④.
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,G在AD上,且DF=BE.①CE=CF;②EC⊥CF;③△ECG≌△FCG,④若∠GCE=45°,则EG=BE+GD,以上说法正确的是①②④.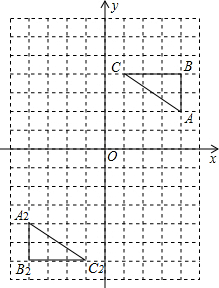 如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,点A的坐标(4,2)
如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,点A的坐标(4,2)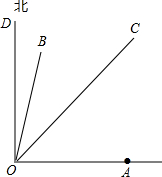 如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A.
如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A.