题目内容
12.计算:($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)分析 把($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)化为(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)+(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)求解即可.
解答 解:($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)
=(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)
=(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)+(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)
=-(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2004}$)+(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2003}$)
=-$\frac{1}{2004}$.
点评 本题主要考查了有理数的混合运算,解题的关键是找出式子的规律化简.

| A. | $\sqrt{5}$ | B. | $\sqrt{34}$ | C. | $\sqrt{17}$ | D. | 均不是 |
 如图所示,已知∠1=60°,∠2+∠3=180°,∠3=∠4,你能否求出∠5的度数?试试看.
如图所示,已知∠1=60°,∠2+∠3=180°,∠3=∠4,你能否求出∠5的度数?试试看. 如图所示,在等腰△ABC中,AB=AC=6,cosB=$\frac{1}{3}$,求BC和tanB的值.
如图所示,在等腰△ABC中,AB=AC=6,cosB=$\frac{1}{3}$,求BC和tanB的值. 如图,C是线段AB上的一点,D是线段CB的中点,已知AC=p,且p,q,r为质数,p<q,p+q=r,又知图中所有线段长度之和为27,则线段AB的长是( )
如图,C是线段AB上的一点,D是线段CB的中点,已知AC=p,且p,q,r为质数,p<q,p+q=r,又知图中所有线段长度之和为27,则线段AB的长是( )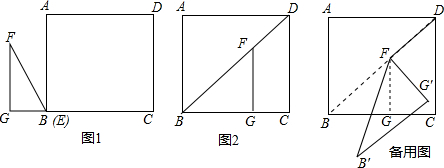
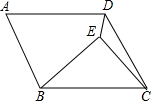 如图,在?ABCD内有一点E,如果满足∠EDA=90°,∠EBC=∠EDC,∠ECB=45°,试问是否有与BE相等的线段?
如图,在?ABCD内有一点E,如果满足∠EDA=90°,∠EBC=∠EDC,∠ECB=45°,试问是否有与BE相等的线段?