题目内容
2.已知a,b,c是三角形的三边长,a=m2-n2,b=2mn,c=m2+n2,(m,n为任意正整数,m>n),试说明△ABC为直角三角形.分析 判断一组数能否成为直角三角形的三边,就是看是否满足两较小边的平方和等于最大边的平方.
解答 解:∵(m2-n2)2+(2mn)2=m4+n4-2m2n2+4m2n2=m4+n4+2m2n2=(m2+n2)2,
∴a2+b2=c2,
∴△ABC为直角三角形.
点评 本题考查了勾股定理的逆定理的应用,在应用时注意是两较短边的平方和等于最长边的平方.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
7.$\sqrt{{x}^{2}+2x+2}$+$\sqrt{(x-2)^{2}+16}$的最小值为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{34}$ | C. | $\sqrt{17}$ | D. | 均不是 |
13.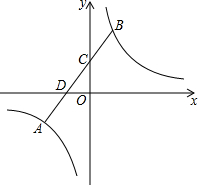 如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
 如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )| A. | AD>BC | B. | AD=BC | C. | AD<BC | D. | 无法判断 |

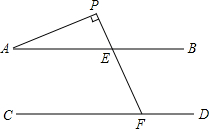 如图,直线AB∥CD,∠P=90°,试求∠EFD-∠A的度数,并写出每一步的依据.
如图,直线AB∥CD,∠P=90°,试求∠EFD-∠A的度数,并写出每一步的依据.