题目内容
7.已知点A、B、C、D在⊙O上,AB∥CD,AB=24,CD=10,⊙O的半径为13,求梯形ABCD的面积.分析 根据题意画出图形,进而分类讨论得出EF的长,进而求出面积即可.
解答 解:如图1所示:过点O作OE⊥CD,OF⊥AB,
且EF必过点O,
∵AB∥CD,AB=24cm,CD=10cm,圆O的直径为26cm,
∴EC=5cm,BF=12cm,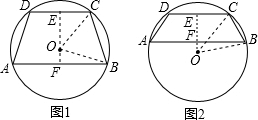
∴EO=12cm,FO=5cm,
则EF=17cm,
故梯形ABCD的面积为:$\frac{1}{2}$(10+24)×17=289(cm2),
如图2,同理可得出:EF=12-5=7(cm),
则梯形ABCD的面积为:$\frac{1}{2}$(10+24)×7=119(cm2).
综上所述:梯形ABCD的面积为289cm2或119cm2.
点评 此题考查了垂径定理,勾股定理,利用了分类讨论的思想,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若$\sqrt{(x-3)^{2}}$+3=x,则x的取值范围是( )
| A. | x<3 | B. | x≤3 | C. | x>3 | D. | x≥3 |
2.四边形ABCD中,∠A=∠B=∠C=90°,下列条件能使这个四边形是正方形的是( )
| A. | ∠D=90° | B. | AB=CD | C. | BC=CD | D. | AC=BD |
12.在?ABCD中,∠B+∠D=260°,那么∠A的度数是( )
| A. | 130° | B. | 100° | C. | 50° | D. | 80° |
 如图,菱形ABCD的周长为32,对角线AC、BD相交于点O,E为BC的中点,则OE=4.
如图,菱形ABCD的周长为32,对角线AC、BD相交于点O,E为BC的中点,则OE=4. 如图,AD是△ABC的高,AE是中线,若AD=5,CE=4,则△AEB的面积为10.
如图,AD是△ABC的高,AE是中线,若AD=5,CE=4,则△AEB的面积为10. 如图,已知四边形ABCD是矩形,对角线AC,BD交于点O,CE∥BD,DE∥AC,CE与DE交于点E,请探索DC与OE的位置关系,并说明理由.
如图,已知四边形ABCD是矩形,对角线AC,BD交于点O,CE∥BD,DE∥AC,CE与DE交于点E,请探索DC与OE的位置关系,并说明理由. 已知:如图,在矩形ABCD中,点E是BC边上一点,且AE=DE.
已知:如图,在矩形ABCD中,点E是BC边上一点,且AE=DE.