题目内容
2．四边形ABCD中，∠A=∠B=∠C=90°，下列条件能使这个四边形是正方形的是（ ）| A． | ∠D=90° | B． | AB=CD | C． | BC=CD | D． | AC=BD |
分析 根据题意得到四边形ABCD为矩形，再由邻边相等的矩形为正方形即可得证．
解答 解：四边形ABCD中，∠A=∠B=∠C=90°，能使这个四边形是正方形的是BC=CD，
故选B
点评 此题考查了正方形的判定，熟练掌握正方形的判定方法是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知?ABCD中，AE平分∠BAD，CF平分∠BCD，分别交BC、AD于E、F．求证：AF=EC．
如图，已知∠A=20°，∠B=37°，AC⊥DE，垂足为F，求∠1，∠D的度数．
甲、乙、丙、丁四人进行飞镖比赛，已知他们每人五次投得的成绩如图所示，那么四人中成绩最稳定的是（ ）
17．
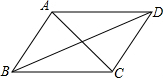如图，已知?ABCD，在分别以四个顶点为起点和终点的向量中，向量$\overrightarrow{BD}$=（ ）
如图，已知?ABCD，在分别以四个顶点为起点和终点的向量中，向量$\overrightarrow{BD}$=（ ）| A． | $\overrightarrow{BA}$+$\overrightarrow{BC}$ | B． | $\overrightarrow{AB}$+$\overrightarrow{CB}$ | C． | $\overrightarrow{AB}$+$\overrightarrow{BC}$ | D． | $\overrightarrow{AB}$-$\overrightarrow{BC}$ |
14．
如图，在矩形ABCD中，AB=2BC，在CD上取一点E，使AE=AB，则∠EBC等于（ ）
如图，在矩形ABCD中，AB=2BC，在CD上取一点E，使AE=AB，则∠EBC等于（ ）| A． | 10° | B． | 15° | C． | 22.5° | D． | 30° |