题目内容
18．若$\sqrt{（x-3）^{2}}$+3=x，则x的取值范围是（ ）| A． | x＜3 | B． | x≤3 | C． | x＞3 | D． | x≥3 |
分析 已知等式变形后，利用二次根式性质确定出x的范围即可．
解答 解：已知等式整理得：$\sqrt{（x-3）^{2}}$=|x-3|=x-3，
∴x-3≥0，
解得：x≥3，
故选D
点评 此题考查了二次根式的性质与化简，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
9．
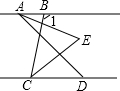如图，己知 AB∥CD，∠BAD 和∠BCD 的平分线交于点E，∠1=100°，∠BAD=m°，则∠AEC的度数为（ ）
如图，己知 AB∥CD，∠BAD 和∠BCD 的平分线交于点E，∠1=100°，∠BAD=m°，则∠AEC的度数为（ ）| A． | m° | B． | （40+$\frac{m}{2}$）° | C． | （40-$\frac{m}{2}$）° | D． | （50+$\frac{m}{2}$）° |
6．
如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD，若BD=2，则AB的长是（ ）
如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD，若BD=2，则AB的长是（ ）| A． | 2$\sqrt{3}$ | B． | 4 | C． | 4$\sqrt{3}$ | D． | 6 |
如图，已知∠A=20°，∠B=37°，AC⊥DE，垂足为F，求∠1，∠D的度数．
已知函数y=kx+b的图象与x轴、y轴分别交于点A（12，0）、点B，与函数y=x的图象交于点E，点E的横坐标为3，求：
甲、乙、丙、丁四人进行飞镖比赛，已知他们每人五次投得的成绩如图所示，那么四人中成绩最稳定的是（ ）