题目内容
15．
如图，AD是△ABC的高，AE是中线，若AD=5，CE=4，则△AEB的面积为10．
分析 由三角形的中线的定义可得BE=CE=4，再根据三角形的面积公式即可求得△AEB的面积．
解答 解：∵AE是△ABC的中线，CE=4，
∴BE=CE=4，
又∵高AD=5，
∴S△AEB=$\frac{1}{2}$•BE•AD=$\frac{1}{2}$×4×5=10．
故答案为：10．
点评 此题考查三角形的面积公式，三角形的中线的定义，关键是掌握三角形的面积等于底与高乘积的一半．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
已知：如图，AB∥CD，∠A=∠D，试说明 AC∥DE 成立的理由．
6．
如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD，若BD=2，则AB的长是（ ）
如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD，若BD=2，则AB的长是（ ）| A． | 2$\sqrt{3}$ | B． | 4 | C． | 4$\sqrt{3}$ | D． | 6 |
已知函数y=kx+b的图象与x轴、y轴分别交于点A（12，0）、点B，与函数y=x的图象交于点E，点E的横坐标为3，求：
甲、乙、丙、丁四人进行飞镖比赛，已知他们每人五次投得的成绩如图所示，那么四人中成绩最稳定的是（ ）
20．
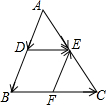如图，已知在△ABC中，点D、E、F分别是AB、AC、BC的中点．下列结论不正确的是（ ）
如图，已知在△ABC中，点D、E、F分别是AB、AC、BC的中点．下列结论不正确的是（ ）| A． | $\overrightarrow{DE}$∥$\overrightarrow{BC}$ | B． | $\overrightarrow{AD}-\overrightarrow{AE}=\overrightarrow{DE}$ | C． | $\overrightarrow{DB}$=$-\overrightarrow{FE}$ | D． | $\overrightarrow{DB}+\overrightarrow{DE}+\overrightarrow{FE}=\overrightarrow{DE}$ |
4．某超市一月份的营业额为200万元，三月份的营业额为288万元，如果每月比上月增长的百分数相同，则平均每月的增长（ ）
| A． | 10% | B． | 15% | C． | 20% | D． | 25% |